Систему называют замкнутой (изолированной), если действием внешних сил можно пренебречь в сравнении с внутренними силами.
Закон сохранения импульса
Закон сохранения импульса позволяет без рассмотрения сил, которые оказывают действие на тела, и не рассматривая детально движение тел, решать некоторые практические задачи. Существуют ситуации, когда законы Ньютона не применимы для решения задач, однако законы сохранения не теряют своего значения. Всеобщность законов сохранения делает их важными.
Закон сохранения импульса в замкнутых системах
В замкнутых системах справедлив закон сохранения импульса: суммарный импульс замкнутой системы тел не изменяется при любых процессах, происходящих в системе. Это не означает, что неизменным является импульс каждого тела, входящего в систему. Из-за действия внутренних сил, импульсы тел, находящихся внутри рассматриваемой системы, изменяются все время. Постоянной остается только векторная сумма импульсов всех частей из которых состоит система.
Допустим, что система состоит из двух тел. В момент времени $t'$ импульс первого тела равен ${\overline{p}}'_1$, второго ${\overline{p}}'_2$. В момент времени $t''$ первое тело стало обладать импульсом ${\overline{p}}^{''}_1$, а второе ${\overline{p}'}'_2$. Система из наших двух тел является замкнутой. Тогда закон сохранения импульса запишем как:
\[{\overline{p}}'_1+{\overline{p}}'_2={\overline{p}}^{''}_1+{\overline{p}'}'_2\left(1\right).\]Для изолированной системы имеющей N тел закон сохранения импульса принимает вид:
\[\sum\limits^N_{i=1}{{\overline{p}}_i=const\ \left(2\right).}\]Принимая во внимание то, что импульс тела определен как:
\[{\overline{p}}_i=m_i{\overline{v}}_i\left(3\right),\]где $m_i$ - масса $i-го$ тела; ${\overline{v}}_i$ - его скорость, закон сохранения импульса можно представить как:
\[\sum\limits^N_{i=1}{m_i{\overline{v}}_i=const\ \left(4\right).}\]Закон сохранения импульса является следствием второго и третьего законов Ньютона. Закон сохранения импульса является фундаментальным законом. Он связан с однородностью пространства, в котором все точки равноправны. Пространственный сдвиг механической системы не влияет на процессы, которые в этой системе происходят.
Следует помнить, что если система тел является незамкнутой, но действие внешних сил на тела системы взаимно компенсируются, то закон сохранения импульса выполняется. Если сумма внешних сил не равна нулю, но равной нулю является суммарная проекция этих сил на какое - то направление, то проекция импульса системы на это направление сохраняется. Например, имеется некоторая система тел около поверхности Земли. Эта система не может быть замкнутой, так как все тела системы испытывают действие силы тяжести. Сила тяжести изменяет импульсы тел системы по вертикали. Но по горизонтальному направлению сила тяжести не изменяет импульсы тел, следовательно, сумма проекций импульсов тел данной системы на горизонтальную ось будет постоянной, если не учитывать силы сопротивления.
Если взаимодействия происходят с большой скоростью (столкновения атомов, взрывы т.д.) считают, что изменение импульсов отдельных тел происходят за счет внутренних сил. Импульс системы в этих случаях сохраняется с высокой точностью, так как сила тяжести и силы сопротивления не оказывают существенного влияния на изменение импульса такой системы (эти силы малы в сравнении с внутренними силами).
Большое значение закон сохранения импульса имеет при изучении реактивного движения. Закон сохранения импульса часто применяют при решении задач, в которых следует отыскать скорость, а не силы или ускорения. Такие задачи в классической механике можно решить при помощи законов Ньютона, но использование законов сохранения позволяет упростить их решение.
Примеры задач с решением
Задание. Снаряд массой $m=20\ $кг имел скорость $v=$300 $\frac{м}{с}$. Он разорвался на две части. Одна из них массой $m_1=5$ кг продолжила движение в прежнем направлении со скоростью $v_1=$ 500 $\frac{м}{с}$. Какой была скорость второй части снаряда сразу после взрыва?
Решение. Сделаем рисунок.
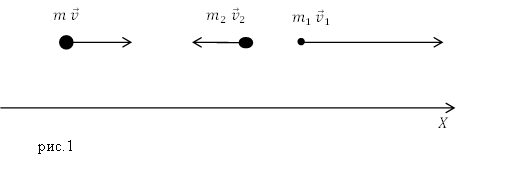
Закон сохранения импульса в нашей задаче применять можно, так как действием внешних сил можно пренебречь, в сравнении c большими внутренними силами, действующими в системе при взрыве. Запишем закон сохранения в векторном виде:
\[m\overline{v}=m_1{\overline{v}}_1+m_2{\overline{v}}_2\left(1.1\right).\]Спроектируем выражение (1.1) на ось X рис.1:
\[mv=m_1v_1-m_2v_2\left(1.2\right).\]Массу второго куска снаряда найдем как:
\[m_2=m-m_1\left(1.3\right).\]Из формулы (1.2) получим:
\[v_2=\frac{m_1v_1-mv}{m_2}=\frac{m_1v_1-mv}{m-m_1}.\]Вычислим искомую скорость:
\[v_2=\frac{5\cdot 500-20\cdot 300}{20-5}\approx -233\ (\frac{м}{с}).\]Ответ. $v_2=233\ \frac{м}{с}$, скорость направлена против оси X (рис.1)
Задание. По рельсам, в горизонтальном направлении катится платформа массой $M$. Скорость платформы равна $v.$ На нее сверху поставили груз массой $m$. Какова стала скорость платформы?
Решение. Сделаем рисунок.
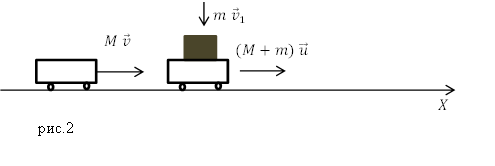
Данную систему считать замкнутой нельзя, однако по горизонтали, импульс системы сохраняется, так как сила тяжести, действующая вертикально на груз не может изменять импульс в этом направлении, поэтому запишем:
\[Mv=\left(M+m\right)u\left(2.1\right).\]Из выражение (2.1) получим:
\[u=\frac{Mv}{m+m}.\]Ответ. $u=\frac{Mv}{m+m}$
Читать дальше: звук.










