Отклонение от прямолинейного распространения волны, огибание волной препятствия называют дифракцией.
Примеры дифракции
Дифрагировать могут любые волны (волны света, акустические волны и др.). Явление дифракции проявляется особенно четко, если размеры препятствий сравнимы или меньше длины волны. При дифракции поверхность волны искривляется около краев препятствия.
Дифракцию объясняют с помощью принципа Гюйгенса. Каждую точку волнового поля нужно рассматривать в качестве источника вторичных волн. Эти волны распространяются во всех направлениях, попадая в область геометрической тени препятствия.
Дифракция механических волн
Рассмотрим дифракцию волн на поверхности воды. На пути распространения волн поместим экран, имеющий узкую щель. Размер щели меньше длины волны. За экраном будет распространяться круговая волна так, как будто в щели находится источник волн, как и следует из принципа Гюйгенса. Вторичные источники в узком отверстии экрана находятся близко друг к другу и их можно считать единым точечным источником.
Увеличим размер отверстия в экране до величины много большей длины волны. Картина распространения волн за экраном станет иной. Волна будет проходить через щель, не изменяя своей формы. На краях отверстия экрана можно заметить только небольшое искривление поверхности волны, волна частично попадает в пространство позади экрана.
Дифракция световых волн
Исторически явление дифракции начали исследовать при изучении свойств света.
Дифракция света - это совокупность явлений, которые связаны с волновой природой света. Дифракцию света можно получить при распространении его в веществе, имеющем неоднородности. Примерами дифракции света являются: отклонение света от распространения по прямой линии при прохождении через отверстие в непрозрачном экране, огибание границ непрозрачных тел.
Наблюдать дифракцию света - это непростая задача, так как длина световой волны мала, тогда как световые волны отклоняются от распространения по прямой на заметные углы, только на препятствиях, которые сравнимы с длиной волны. Все же явление дифракции можно наблюдать, если пропустить луч света сквозь малое отверстие. При этом светлое пятно на экране наблюдения будет больше, чем поперечное сечение луча.
Классический опыт по наблюдению явления дифракции поставил Т. Юнг.
В непрозрачном экране он сделал два маленьких отверстия (рис.1) B и С на некотором расстоянии друг от друга. Свет на эти отверстия попадал после прохождения через малое отверстие A, которое было сделано в другом экране. Сферическая волна, которая распространялась от отверстия А возбуждала в отверстиях В и С когерентные колебания. В результате дифракции от отверстий B и С выходили два световых конуса, которые частично накладывались друг на друга. В результате интерференции двух волн света от источников B и C на экране возникала совокупность светлых и темных полос. При закрытии одного из отверстий интерференционные полосы исчезали.
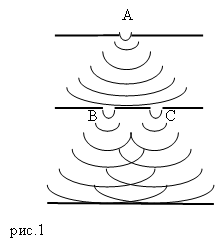
В результате явления дифракции вместо тени от тонкой проволоки на экране можно наблюдать совокупность светлых и темных полос. В центре картины дифракции от отверстия можно видеть темное пятно, которое окружают светлые и темные кольца. В центре тени, которую образует круглый экран, можно наблюдать светлое пятно, при этом тень о экрана будет окружена темными концентрическими кольцами.
Дифракционная решетка
На основе явления дифракции основывается устройство дифракционной решетки. Этот простейший оптический прибор является совокупностью узких щелей, которые разделяют узкие непрозрачные промежутки. Величины углов ($\varphi $), получаемых при направлении на максимумы спектра дифракции, появляющиеся при использовании дифракционной решетки определяет формула:
\[d\ sin\ \varphi =\pm k\lambda \ \left(k=0,1,2\dots \right)\left(1\right),\]где $d$ - период решетки. С помощью дифракционной решетки белый свет раскладывается в спектр. Дифракционную решетку можно использовать для вычисления длины света.
Примеры задач с решением
Задание. Какова длина волны света, которым освещают отверстие экранов в опыте Юнга, если расстояние между щелями B и С равно $d$, расстояние между экраном на котором расположены щели и экраном наблюдения D, между соседними светлыми дифракционными полосами расстояние равно $\Delta h$?
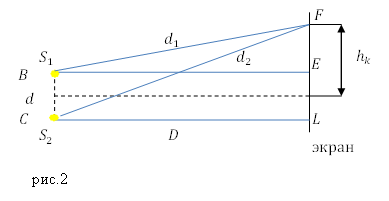
Решение. Источники волн находятся в отверстиях B и C и обозначены на рис.2 как $S_1$ и $S_2$. На экране наблюдения максимум освещенности будет в точке F, если для нее выполняется условие:
\[d_2-d_1=m\lambda \left(1.1\right),\]где $m=0,1,..$ целые числа. Рассмотрим треугольник $S_1FE$, по теореме Пифагора, для его стороны $d_1$ запишем:
\[d^2_1=D^2+{\left(h_k-\frac{d}{2}\right)}^2\left(1.2\right).\]Из треугольника $S_2FL$ имеем:
\[d^2_2=D^2+{\left(h_k+\frac{d}{2}\right)}^2\left(1.3\right).\]Найдем разность между уравнениями (1.2) и (1.3):
\[d^2_2-d^2_1=2h_kd\ \to \left(d_2-d_1\right)\left(d_2+d_1\right)=2h_kd\left(1.4\right).\]Учитывая, что расстояние между источниками волн много меньше, чем расстояние от источников до экрана наблюдения можно положить, что:
\[d_2+d_1\approx 2D\to d_2-d_1\approx \frac{h_kd}{D}\left(1.5\right).\]Принимая во внимание выражение (1.1) и (1.5) получим:
\[m\lambda =\frac{h_kd}{D}\left(1.6\right).\]Из формулы (1.6) получим расстояние от центра экрана наблюдения до светлой полосы номер $m$:
\[h_k=\frac{m\lambda D}{d}\left(1.7\right).\]Тогда расстояние между соседними светлыми полосами равно:
\[\Delta h=h_{k+1}-h_k=\frac{лD}{d}\left(1.8\right).\]Из (1.8) выразим искомую длину волны:
\[\lambda =\frac{d\Delta h}{D}.\]Ответ. $\lambda =\frac{d\Delta h}{D}$
Задание. На дифракционную решетку с периодом дифракции равным $d$ нормально падает плоская монохроматическая волна света (длина волны $\lambda $). Каков самый большой порядок спектра, который можно наблюдать в данном случае?
Решение. Основой для решения задачи служит формула:
\[d\ sin\ \varphi =k\lambda \left(2.1\right).\]Максимальному значению $k$ (это и есть максимальный порядок спектра дифракции) соответствует значение синуса равное единице, то есть:
\[d=k\lambda \left(2.2\right).\]Из (2.2) $k$ равно:
\[k=\frac{d}{\lambda }.\]Ответ. $k=\frac{d}{\lambda }$
Читать дальше: принцип Бабине.










