Полупроводниками называют вещества, чья электропроводность меньше электропроводности металлов и больше электропроводности диэлектриков.
Зонная структура полупроводников
Определение
Полупроводники при температуре около абсолютного нуля имеют полную занятость электронами валентной зоны, которая отделена от зоны проводимости относительно узкой запрещенной зоной ($\Delta E\sim 1эВ$).
Полупроводники делят на собственные и примесные.
Собственные полупроводники
Определение
Собственные полупроводники - это химически чистые вещества, их проводимость называют собственной.
При $T=0K$ собственные полупроводники работают как диэлектрики. С ростом температуры электроны, находящиеся на верхних уровнях валентной зоны (1) могут переходить на нижние уровни зоны проводимости (2) рис.1. При помещении полупроводника во внешнее электрическое поле электроны движутся против поля, создавая электрический ток. Зона 2 становится зоной проводимости. Проводимость собственных полупроводников называют электронной (проводимостью $n$ - типа).
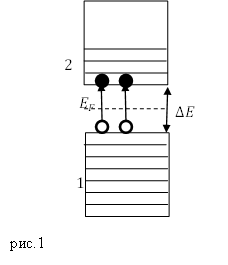
В результате перехода электронов из зоны 1 в зону 2 в валентной зоне возникают вакантные состояния, которые называют дырками. При наличии внешнего электрического поля на освободившееся от электрона место может перейти электрон с соседнего уровня, тогда дырка возникнет там, откуда переместился электрон. Данный процесс, при котором дырки заполняются электронами, эквивалентен движению дырки против перемещения электрона. Проводимость, которая обусловлена перемещением дырок называют дырочной проводимостью (проводимость -типа).
Так, получаем, что в собственных полупроводниках имеется два механизма проводимости: $n$ - типа и -типа. Количество электронов в зоне проводимости равно числу дырок в валентной зоне.
Зонная структура полупроводников
Проводимость полупроводников проявляется только при воздействии внешних факторов.
У собственных полупроводников уровень Ферми лежит в середине запрещенной зоны рис.1. Для перескока электрона с верхнего уровня валентной зоны на нижний уровень зоны проводимости необходимо потратить энергию активации, которая равна ширине запрещенной зоны ($\Delta E$). При переходе электрона в зону проводимости в валентной зоне возникает дырка, значит, энергия, которая тратится на возникновение пары носителей тока делится на два. Энергия, равная половине запрещенной зоны тратится на переброс электрона, равная ей энергия идет на образование дырки, следовательно, начало отсчета для этих процессов лежит посередине запрещенной зоны.
Удельная проводимость ($\gamma $) собственных полупроводников равна:
\[\gamma ={\gamma }_0e^{-\frac{\Delta E}{2kT}}\left(1\right),\]где ${\gamma }_0$ - постоянная, свойственная конкретному полупроводнику.
Одним из самых распространенных полупроводников является германий, который имеет решетку, в которой каждый атом имеет связь при помощи ковалентных связей с четырьмя «соседями».
Примеры задач с решением
Пример 1
Задание. Как объясняется увеличение проводимости собственных полупроводников с ростом температуры с точки зрения зонной теории?
Решение. Зонная теория объясняет повышение проводимости полупроводников при увеличении температуры тем, что количество электронов, которые в результате теплового возбуждения переходят в зону проводимости, растет, и они принимают участие в процессе проводимости.
Рассмотрим формулу, связывающую удельную проводимость собственного полупроводника и его температуру:
\[\gamma ={\gamma }_0e^{-\frac{\Delta E}{2kT}}\left(1.1\right).\]Прологарифмируем обе части выражения (1.1), получим:
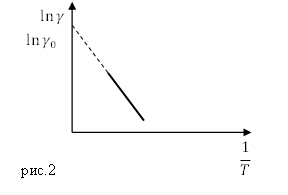
\[{\ln (\gamma )\ }={\ln \left({\gamma }_0\right)\left(-\frac{\Delta E}{2kT}\right)\ }\left(1.2\right).\]Из формулы (1.2) мы видим, что ${\ln (\gamma )\ }\sim \frac{1}{T}$. На рис.2 данную зависимость изобразим прямой. Угол наклона прямой ${{\rm ln\ }\gamma (\frac{1}{T})\ }$ задет ширина запрещенной зоны $\Delta E$. Продолжив прямую ${{\rm ln\ }\gamma (\frac{1}{T})\ }$ до пересечения с осью ${\rm ln\ }\gamma $ полуим ${\ln ({\gamma }_0)\ }$.
Пример 2
Задание. Что происходит с кристаллом германия, если повышать его температуру.
Решение. Идеальный кристалл германия при температуре близкой к абсолютному нулю является диэлектриком, поскольку все валентные электроны принимают участие в образовании валентных связей и не могут участвовать в проводимости.
Будем увеличивать температуру данного полупроводника. При этом тепловые колебания решетки ведут к разрыву некоторых валентных связей. Часть электронов отсоединяется, и они становятся свободными. На том месте, где был электрон, возникает «дырка». Эти «дырки» могут заполнять электроны из соседних пар. В результате данного процесса дырка, как и электрон, движется по полупроводнику. Если внешнего электрического поля нет, то электроны и дырки совершают хаотические движения. При наложении поля на полупроводник электроны станут двигаться против внешнего поля, а дырки по полю, при этом появляется собственная проводимость германия, вызванная движением, как электронов, так и дырок.
Для каждой температуры устанавливается определённая равновесная концентрация электронов и дырок, зависящая от температуры.
Читать дальше: зоны Френеля, векторная диаграмма.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Статьи по теме
Поможем выполнить
любую работу
