Задачи и методы термодинамики в физике
Задачи и методы термодинамики
Задачи термодинамики
Термодинамические системы являются макросистемами, состоящими из огромного количества частиц, совершающих сложные движения.
Задачей термодинамики считают изучение свойств термодинамических систем и описание их при помощи макроскопических величин, применяя всеобщие законы, которые называют началами термодинамики. В термодинамике не рассматривают причины возникновения тех или иных термодинамических явлений с точки зрения микромира. Термодинамика основывается на трех началах.
Первое начало - это применение закона сохранения энергии к термодинамическим явлениям. Второе начало определяет направление развития процессов, которые рассматривает термодинамика. Третье начало накладывает ограничения на процессы, постулируя невозможность процессов, которые привели бы к достижению термодинамического нуля температуры.
Метод термодинамики
В молекулярной физике используют два способа описания процессов, которые происходят в макроскопических телах: статистический и термодинамический методы.
В качестве модели вещества, на которой рассматривается большинство примеров применения термодинамического метода, используют модель идеального газа. Но сам термодинамический метод применим и к реальным веществам.
Термодинамический метод рассматривает взаимодействие тел с энергетической точки зрения. Он определяет соотношение между параметрами термодинамических систем. В основании термодинамики лежат небольшое число фундаментальных законов, которые получены эмпирическим путем, методом обобщения множественных фактов.
Отличие термодинамического метода состоит в том, что он не связан с конкретным представлением о строении тела и характером перемещения частиц. Термодинамика использует макроскопические параметры для описания состояния систем. Термодинамический метод применяют для теоретического исследования самых общих законов явлений. Методы термодинамики обладают большой строгостью. Это является для термодинамики достоинством и проблемой одновременно, так как, имея такое свойство как общность, термодинамика не может вывести частные законы, которые характеризовали бы специфичные свойства некоторых систем. Термодинамический метод дополняют молекулярно -кинетической теорией.
Термодинамику строят на принципах дедукции, от общего (трех начал) к частному.
Основными физическими величинами в термодинамике являются: количество теплоты (Q), внутренняя энергия (U), работа (A), энтропия (S), энтальпия (H).
Работу газа при равновесном расширении находят как:
\[A=\int\limits^{V_2}_{V_1}{pdV\ \left(1\right),}\]
где $p$ - давление; $V$ - объем.
Малое количество теплоты $\delta Q$, определяют как:
\[\delta Q=CdT\left(2\right),\]
где C - теплоемкость тела; $T$ - термодинамическая температура.
Работа и количество теплоты в общем случае- функции процесса.
Внутренняя энергия ($U$) является функцией состояния термодинамической системы, она определяется:
\[U=W-\left(E_k+E^{vn}_p\right)\left(3\right),\]
где $W$- полная энергия системы, $E_k$- кинетическая энергия макроскопического движения системы, $E^{vn}_p$- потенциальная энергия системы, которая является результатом, действия на систему внешних сил.
Внутреннюю энергию идеального газа находят как:
\[U=\int\limits^T_0{\frac{i}{2}\nu RdT\left(4\right),}\]
где $i$ - число степеней свободы молекулы, $\nu $ - количество вещества, $R$ - газовая постоянная.
Энтропия - это еще одна функция состояния термодинамической системы. Элемент энтропии при совершении обратимого процесса равен:
\[dS=\frac{\delta Q}{T}\left(5\right).\]
В термодинамике рассматривают термодинамически равновесные состояния системы или процессы, которые можно представить как совокупность равновесных состояний.
Теория дифференциальных уравнений и уравнения в частных производных является математическим аппаратом, используемым в термодинамике.
Примеры задач с решением
Пример
Задание. Какова удельная теплоемкость при постоянном объеме смеси двух газов, если массы первого газа $m_1$, масса второго газа $m_2$, величины удельных теплоемкостей каждого газа равны: $c_{V1}\ $и $c_{V2}$?
Решение. Количество теплоты ($\Delta Q$), которое необходимо для нагревания смеси газов, если температура смеси изменяется на величину $\Delta T$ найдем как:
\[\Delta Q=c_V\left(m_1+m_2\right)\Delta T\left(1.1\right),\]
где $c_V$ - искомая теплоемкость смеси газов.
Количество теплоты, которое подводят к смеси $\Delta Q$ равно сумме теплот, получаемых каждой компонентой смеси:
\[\Delta Q=\Delta Q_1+\Delta Q_2\ \left(1.2\right).\]
$\Delta Q_1$ найдем как:
\[\Delta Q_1=c_{V1}m_1\Delta T\ \left(1.3\right).\]
$\Delta Q_2$ равно:
\[\Delta Q_2=c_{V2}m_2\Delta T\ \left(1.4\right).\]
Используя записанные формулы получим:
\[c_V\left(m_1+m_2\right)\Delta T=c_{V1}m_1?T+c_{V2}m_2\Delta T\ \to c_V=\frac{c_{V1}m_1+c_{V2}m_2}{m_1+m_2}.\]
Ответ. $c_V=\frac{c_{V1}m_1+c_{V2}m_2}{m_1+m_2}$
Пример 2
Задание. Какая работа совершается идеальным газом в процессе 1-2-3, который представлен на рис.1?
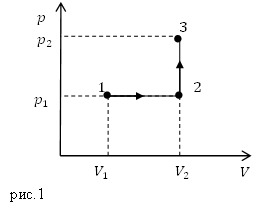
Решение. Рассматривая график можно сделать вывод, что в процессе 2-3 газ работы не совершает, так как объем его постоянный. Работа совершается газом в процессе изобарного расширения (1-2).
Основой для решения задачи примем формулу:
\[A=\int\limits^{V_2}_{V_1}{pdV\ \left(2.1\right).}\]
Так как процесс является изобарным (давление постоянно), то интеграл (2.1) преобразуется к виду:
\[A=p_1\left(V_2-V_1\right).\]
Ответ. $A=p_1\left(V_2-V_1\right)$
Читать дальше: закон сохранения энергии для цепей постоянного тока содержащих ЭДС.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 452 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!











