Центростремительным ускорением называют компоненту полного ускорения материальной точки, движущейся по криволинейной траектории, которая определяет быстроту изменения направления вектора скорости.
Формула центростремительного ускорения
Определение и формула центростремительного ускорения
Другой компонентой полного ускорения является тангенциальное ускорение, оно отвечает за изменение величины скорости. Обозначают центростремительное ускорение, обычно ${\overline{a}}_n$. Центростремительное ускорение еще называют нормальным.
Центростремительное ускорение равно:
\[{\overline{a}}_n=\frac{v^2}{r^2}\overline{r\ }=\frac{v^2}{r}{\overline{e}}_r\left(1\right),\]где ${\overline{e}}_r=\frac{\overline{r\ }}{r}$ - единичный вектор, который направлен от центра кривизны траектории к рассматриваемой точке; $r$ - радиус кривизны траектории в месте нахождения материальной точки в рассматриваемый момент времени.
Первым верные формулы для вычисления центростремительного ускорения получил Х. Гюйгенс.
Единицей измерения центростремительного ускорения в Международной системе единиц является метр, деленный на секунду в квадрате:
\[\left[a_n\right]=\frac{м}{с^2}.\]Формула центростремительного ускорения при равномерном движении точки по окружности
Рассмотрим равномерное движение материальной точки по окружности. При таком перемещении величина скорости материальной точки неизменна ($v=const$). Но это не означает, что полное ускорение материальной точки при таком виде движения равно нулю. Вектор мгновенной скорости направлен по касательной к окружности, по которой перемещается точка. Следовательно, в этом движении скорость постоянно изменяет свое направление. Отсюда следует, что точка имеет ускорение.
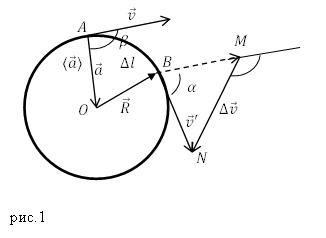
Рассмотрим точки A и B которые лежат на траектории движения частицы. Вектор изменения скорости для точек A и B найдем как:
\[\Delta \overline{v}={\overline{v}}'-\overline{v}\left(2\right).\]Если время, затрачиваемое на движение от точки A до точки B, стремится к нулю, то дуга AB мало не отличается от хорды AB. Треугольники AOB и BMN подобны, получим:
\[\frac{\Delta v}{v}=\frac{\Delta l}{R}=\alpha \left(3\right).\]Величину модуля среднего ускорения определяют как:
\[\left\langle a\right\rangle =\frac{\Delta v}{\Delta t}=\frac{v\Delta l}{R\Delta t}\left(4\right).\]Перейдем к пределу при $\Delta t\to 0\ $ от $\left\langle a\right\rangle \ \ $в формуле (4):
\[a={\mathop{\lim }_{\Delta t\to 0} \left\langle a\right\rangle \ }={\mathop{\lim }_{\Delta t\to 0} \frac{v\Delta l}{r\Delta t}=\frac{v}{R}\ }\mathop{{\rm lim}}_{\Delta t\to 0}\frac{\Delta l}{\Delta t}=\frac{v}{R}v=\frac{v^2}{R}\left(5\right).\]Вектор среднего ускорения составляет с вектором скорости угол равный:
\[\beta =\frac{\pi +\alpha }{2}\left(6\right).\]При $\Delta t\to 0\ $ угол $\alpha \to 0.$ Получается, что вектор мгновенного ускорения составляет с вектором скорости угол $\frac{\pi }{2}$.
И так, что материальная точка, равномерно движущаяся по окружности, обладает ускорением, которое направленно к центру окружности (${\overline{a}}_n\bot \overline{v}$), его величина равна скорости в квадрате, деленной на радиус окружности:
\[a_n=\frac{v^2}{R}={\omega }^2R\ \left(7\right),\]где $\omega $ - угловая скорость движения материальной точки ($v=\omega \cdot R$). В векторном виде формулу для центростремительного ускорения можно записать, опираясь на (7) как:
\[{\overline{a}}_n=-{\omega }^2\overline{R}\ \left(8\right),\]где $\overline{R}$ - радиус-вектор, равный по длине радиусу дуги окружности, направленный от центра кривизны к местоположению рассматриваемой материальной точки.
Примеры задач с решением
Задание. Векторное уравнение $\overline{r}\left(t\right)=\overline{i}{\cos \left(\omega t\right)+\overline{j}{\sin \left(\omega t\right)\ }\ }$, где $\omega =2\ \frac{рад}{с},$ описывает движение материальной точки. По какой траектории движется данная точка? Чему равен модуль ее центростремительного ускорения? Считайте, что все величины в системе СИ.
Решение. Рассмотрим уравнение движения точки:
\[\overline{r}\left(t\right)=\overline{i}{\cos \left(\omega t\right)+\overline{j}{\sin (\omega t)\ }\ }\ \left(1.1\right).\]В декартовой системе координат это уравнение эквивалентно системе уравнений:
\[\left\{ \begin{array}{c} x={\cos \left(\omega t\right);;\ } \\ y={\sin \left(\omega t\right)\ } \end{array} \left(1.2\right).\right.\]Для того, чтобы понять по какой траектории движется точка нам следует исключить время из уравнений системы (1.2). Для этого возведем оба уравнение в квадрат и сложим их:
\[x^2+y^2={cos}^2\left(\omega t\right)+{sin}^2\left(\omega t\right)=1\ \left(1.3\right).\]Из уравнения (1.3) мы видим, что траекторией движения точки является окружность (рис.2) радиуса $R=1$ м.
Для того чтобы найти центростремительное ускорение воспользуемся формулой:
\[a_n=\frac{v^2}{R}\left(1.4\right).\]Модуль скорости определим используя систему уравнений (1.2). Найдем компоненты скорости, которые равны:
\[\left\{ \begin{array}{c} v_x=\frac{dx}{dt}=-\omega {\sin \left(\omega t\right)\ }, \\ v_y=\frac{dy}{dt}=\omega {{\cos \left(\omega t\right)\ } ,\ } \end{array} \right.\left(1.5\right).\]Квадрат модуля скорости будет равен:
\[v^2=v^2_x+v^2_y={\omega }^2\left(1.6\right).\]Из того, какой получился модуль скорости (1.6), мы видим, что наша точка движется по окружности равномерно, следовательно, центростремительное ускорение будет совпадать с полным ускорением.
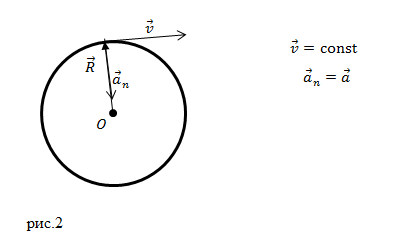
Подставим $v^2$ из (1.6) в формулу (1.4), имеем:
\[a_n=\frac{{\omega }^2}{R}.\]Вычислим $a_n$:
$a_n=\frac{4}{1}=4\ \left(\frac{м}{с^2}\right).$Ответ. 1) Окружность; 2) $a_n=4\ \frac{м}{с^2}$
Задание. Каково центростремительное ускорение точек на ободе диска в момент времени, равный $t=2$c, если диск вращается в соответствии с уравнением: $\varphi (t)=3+2t^3$? Радиус диска равен $R=0,{\rm 1}$ м.
Решение. Центростремительное ускорение точек диска будем искать, применяя формулу:
\[a_n={\omega }^2R\left(2.1\right).\]Угловую скорость найдем, используя уравнение $\varphi (t)=3+2t^3$ как:
\[\omega =\frac{d\varphi }{dt}=6t^2.\ \]При $t=2\ $c угловая скорость равна:
\[\omega \left(t=2\right)=24\ \left(\frac{рад}{с}\right).\]Можно вычислить центростремительное ускорение по формуле (2.1):
\[a_n={24}^2\cdot 0,1=57,6\ \left(\frac{м}{с^2}\right).\]Ответ. $a_n=57,6\frac{м}{с^2}$
Читать дальше: формула циклической частоты колебаний.










