Физика плавания тела, теория и онлайн калькуляторы
Физика плавания тела
На тело, которое находится в жидкости, действуют: сила тяжести, которая направлена вертикально вниз и сила Архимеда, направленная вертикально вверх (рис.1).
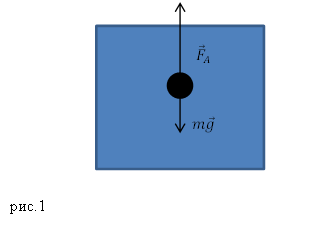
Физика плавания тела
Возможны три варианта движения тела.
- Если сила тяжести ($mg$), действующая на тело больше, чем сила Архимеда ($F_A$), то тело движется вниз (тонет).
- При равенстве $mg=F_A$, тело способно находится в состоянии равновесия в любой точке сосуда с жидкостью (тело плавает).
- В случае если выталкивающая сила больше, силы тяжести тело поднимается в жидкости, то есть всплывает. Когда тело достигает поверхности жидкости, при дальнейшем движении тела сила Архимеда уменьшается, так как она равна:
\[F_A=\rho Vg\ \left(1\right),\]
где $\rho $ - плотность жидкости (газа); $V$ - объем тела, находящийся в веществе; $g$ - ускорение свободного падения. Из формулы (1) видно, что с уменьшением части объема тела в жидкости, уменьшается выталкивающая сила, действующая на тело. Когда сила Архимеда станет равна по модулю силе тяжести, тело перестанет всплывать и будет плавать на поверхности жидкости, частично находясь в ней.
И так, если тело плавает в жидкости, то вес жидкости ($P_g$), которую вытеснило тело, равен его весу ($P$) в воздухе.
Условия плавания тел в жидкости для однородных тел (плотность вещества тела $\rho =const$) можно определить следующим образом:
- Тело тонет, если $\rho >{\rho }_g$ (${\rho }_g-$плотность жидкости).
- ${\rm Тело\ всплывает},\ если\ \ \rho <{\rho }_g$ .
- Если $\rho ={\rho }_g$ тело плавает (находится в равновесии) в жидкости на любой ее глубине.
Для неоднородных тел используют понятие средней плотности, тогда сравнивают ее с плотностью жидкости.
Чем меньше плотность тела в сравнении с плотностью жидкости, тем меньшая его часть находится в жидкости.
Равновесие тел плавающих в жидкости
Если средняя плотность тела меньше плотности жидкости, то часть тела будет выступать над поверхностью. Для плавающих средств имеет большое значение понятие устойчивости плавания. Определяя устойчивость равновесия тела, разделяют случаи: тело полностью погружено в жидкость, тело частично погружено в жидкость.
- Если тело полностью находится в жидкости, и оно плавает в ней (средняя плотность тела равна плотности жидкости), тогда при любых поворотах и смещениях центр масс тела и центр плавучести не изменяют своего положения в отношении тела. Равновесие устойчиво, если центр масс тела находится ниже центра плавучести.
Если бы тело и жидкость были бы абсолютно не сжимаемыми (или их сжимаемости были бы равны), то равновесие тела было бы безразличным. Но в реальности твердые тела имеют, обычно, сжимаемость меньше, чем жидкости. Тела из таких материалов плавают в жидкостях при равенстве плотностей устойчиво.
- Гораздо более сложным является случай, когда тело находится в жидкости не целиком. Когда его часть выступает над свободной поверхностью жидкости. В таком случае смещение тела из положения равновесия вызывает изменение формы вытесняемого телом объема жидкости. Происходит изменение положения центра плавучести в отношении тела. Устойчивость равновесия такого тела определяется при использовании понятие метацентра плавающего тела. Это точка, назовем ее М, которая получается при пересечении вертикальной оси симметрии тела и линии действия выталкивающей силы. Если метацентр находится выше центра масс тела, то момент выталкивающей силы пытается вернуть тело в положение равновесия, это значит, что тело плавает устойчиво. \textbf{}
Примеры задач на плавание тел
Пример 1
Задание. В емкости с водой плавает льдина, внутри которой находится металлический гвоздь (рис.1). Как изменится уровень воды в емкости, после того как лед растает?
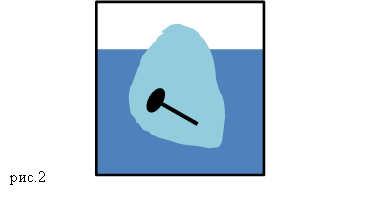
Решение. Плотность металла, из которого изготовлен гвоздь в несколько раз больше, чем плотность воды, допустим, что:
\[\frac{\rho }{{\rho }_{H_2O}}=n\ \left(1.1\right),\]
где $\rho $ - плотность металла гвоздя, ${\rho }_{H_2O}$ - плотность воды. Из условия плавания тел и выражения (1.1) следует, что объем массы воды, которая уравновешивает гвоздь в $n$ раз больше, чем объем гвоздя. После таяния льда гвоздь тонет, но он не заполняет тот объем, который занимал лед вместе с ним. Получаем, что уровень воды в емкости уменьшится.
Ответ. Уменьшится.
Пример 2
Задание. На речной паром, площадь которого равна $S,$ поставили груз. При этом он осел на $h$ м. Какова масса груза?
Решение. Сила Архимеда, которая будет действовать на паром с грузом, равна:
\[F_A=F_{A0}+\rho Vg\ \left(2.1\right),\]
где $F_{A0}$ - сила Архимеда, действующая на паром без груза; $\rho $ - плотность воды в реке; $V$ - изменение объема подводной части парома при размещении на нем груза:
\[V=S\cdot h\ \left(2.2\right).\]
Из условия плавания тел мы можем записать, что сила $F_A$ компенсирует силу тяжести, которая действует на систему груз+ паром:
\[\left(m+m_g\right)g=F_{A0}+\rho Vg\ \left(2.3\right),\]
где $m$ - масса парома; $m_g$ - масса груза. Причем:
\[mg=F_{A0}\left(2.4\right).\]
Следовательно, учитывая (2.2) и (2.4) можно записать, что:
\[m_gg=\rho Vg=\cdot hg\to m_g=\rho Sh.\]
Ответ. $m_g=\rho Sh$
Читать дальше: энергия гармонических колебаний.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 451 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!












