Энергия гармонических колебаний, теория и онлайн калькуляторы
Энергия гармонических колебаний
Рассмотрим превращения энергии, которые происходят при гармонических колебаниях в консервативной системе на примере пружинного маятника.
Потенциальная энергия гармонических колебаний
В процессе механических колебаниях груза на пружине периодически кинетическая энергия ($E_k$) движущегося груза переходит в потенциальную энергию ($E_p$) колебательной системы, состоящей из потенциальной энергии упругодеформированной пружины и потенциальной энергии груза в поле тяжести Земли. Потенциальная энергия пружины при упругой деформации равна:
\[E_{p1}=\frac{k{\left(x+x_0\right)}^2}{2}\left(1\right),\]
где $\left(x+x_0\right)$ - удлинение пружины; $k$ - жесткость пружины.
Потенциальную энергию груза в поле тяжести ($E_{p2}$) найдем как:
\[E_{p2}=-mg\ x+C\left(2\right),\]
где $m$ - масса груза, прикрепленного к пружине.
Постоянную $C,$ будем выбирать так, чтобы в положении равновесия полная потенциальная энергия колебательной системы равнялась:
\[\frac{kx^2_0}{2}+C=0\to C=-\frac{kx^2_0}{2}\ \left(3\right).\]
Тогда потенциальная энергия представлена выражением:
\[E_p=E_{p1}+E_{p2}=\frac{k{\left(x+x_0\right)}^2}{2}-mg\ x-\frac{kx^2_0}{2}=\frac{kx^2}{2}\left(4\right).\]
Кинетическая энергия пружинного маятника
Кинетическая энергия рассматриваемой колебательной системы состоит из энергии движения груза. Используя уравнение смещения груза пружинного маятника при гармонических колебаниях, происходящих по оси X:
\[x=A{\cos \left({\omega }_0t+\varphi \right)(5)\ }\]
найдем уравнение изменения кинетической энергии груза. Для этого найдем скорость движения груза как:
\[v=\frac{dx}{dt}=-A{\omega }_0{\sin \left({\omega }_0t+\varphi \right)\left(6\right).\ }\]
В таком случае кинетическая энергия равна:
\[E_k=\frac{m}{2}A^2{{\omega }_0}^2{{sin}^2 \left({\omega }_0t+\varphi \right)\left(7\right).\ }\]
Полная механическая энергия консервативной колебательной системы
Так как пружинный маятник мы считаем консервативной системой, то механическая энергия ее постоянна:
\[E=E_k+E_p=const\ \left(8\right).\]
Проверим справедливость выражения (8),) непосредственным суммированием правых частей выражений (4) и (7): (учитывая (5))
\[E=\frac{m}{2}A^2{{\omega }_0}^2{{sin}^2 \left({\omega }_0t+\varphi \right)+\ }{\frac{kx^2}{2} =\frac{m}{2}A^2\frac{k}{m}{{sin}^2 \left({\omega }_0t+\varphi \right)+\frac{k}{2}A^2\ }{cos}^2\left({\omega }_0t+\varphi \right)=\frac{k}{2}A^2=\frac{1}{2}m{\omega }^2_0A^2(9)\ },\]
где ${{\omega }_0}^2=\frac{k}{m}$. Формула (9) показывает, что постоянная полная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=\pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:
\[v_x=\pm {\omega }_0A\left(10\right).\]
В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $\frac{E}{2}$ в противофазе друг с другом, частота их колебаний равна $2{\omega }_0$.
\[{E_k =\frac{E}{2}\left[1-{\cos 2({\omega }_0t+\varphi )\ }\right]\left(11\right).\ }\]
\[E_p=\frac{E}{2}\left[1+{cos 2({\omega }_0t+\varphi )\ }\right]\left(12\right).\]
Примеры задач на энергию гармонических колебаний
Пример 1
Задание. Что собой представляет фазовая траектория пружинного маятника, при рассмотрении его как гармонического осциллятора?
Решение. Уравнение фазовой траектории - это уравнение закона сохранения энергии:
\[\frac{kx^2}{2}+\frac{mv^2_x}{2}=E=const\ \left(1.1\right).\]
Разделим обе части выражения (1.1) на $E$ получим:
\[\frac{x^2}{2{E}/{k}}+\frac{v^2_x}{2{E}/{m}}=1\left(1.2\right).\]
Выражение (1.2) - это уравнение эллипса, полуоси которого равны $\sqrt{2{E}/{k}}$ и $\sqrt{2{E}/{m}}$.
Фазовую траекторию часто сопоставляют с графиком потенциальной энергии осциллятора. При этом в верхней части рисунка (рис.1) изображают график потенциальной энергии ($E_p(x)$), в нижней части изображают фазовую траекторию, которая соответствует колебаниям со значением полной энергии равной E, указанной на верхнем графике.
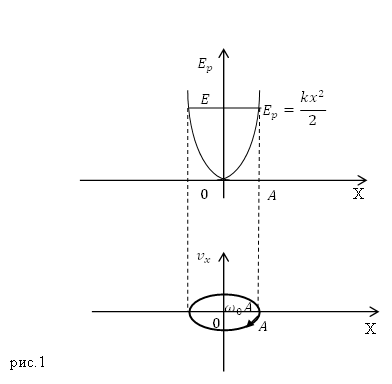
Пример 2
Задание. Материальная точка, имеющая массу $m=5\cdot {10}^{-2}кг,$ совершает колебания в соответствии с законом: $x\left(t\right)={\cos (\frac{3\pi }{2}t)(м)\ }$. Какова полная энергия этой точки?
Решение. Полная энергия в консервативной колебательной системе величина постоянная и найти ее можно в соответствии с выражением:
\[E=\frac{1}{2}m{\omega }^2_0A^2\ \left(2.1\right).\]
Рассматривая уравнение колебаний точки, данное в условии задачи:
\[x\left(t\right)={\cos (\frac{3\pi }{2}t)(м)\ },\]
имеем: $A=1\ м;\ {\omega }_0=\frac{3\pi }{2}$. Вычислим искомую энергию:
\[E=\frac{1}{2}\cdot 5\cdot {10}^{-2}\cdot {\left(\frac{3\pi }{2}\right)}^21^2\approx 0,56\ \left(Дж\right).\]
Ответ. $E=0,56$ Дж
Читать дальше: гидравлический пресс.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 446 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!











