И так, центростремительное ускорение (в общем случае) - это составляющая полного ускорения материальной точки, которая характеризует, как быстро изменяется направление вектора скорости при криволинейном перемещении. Другой компонентой полного ускорения является тангенциальное ускорение, оно отвечает за изменение величины скорости.
Центростремительное ускорение
Центростремительное ускорение при равномерном движении по окружности
Пусть материальная точка равномерно движется по окружности. Тогда модуль ее скорости не изменяется ($v=const$). Но это не значит, что ускорение материальной точки равно нулю. Вектор скорости направлен по касательной к траектории движения точки. При перемещении по окружности скорость изменяет свое направление постоянно. Значит, точка движется с ускорением.
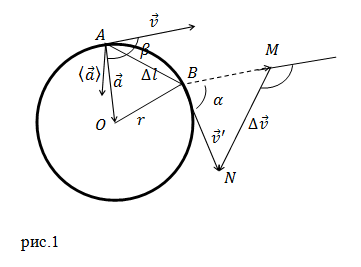
Рассмотрим точки A и B принадлежащие траектории движения рассматриваемого тела. Вектор изменения скорости для этих точек равен:
\[\Delta \overline{v}={\overline{v}}'-\overline{v}\left(1\right).\]Если время движения, между точками A и B мало, то дуга AB мало отличается от хорды AB. Треугольники AOB и BMN подобны, следовательно:
\[\frac{\Delta v}{v}=\frac{\Delta l}{r}=\alpha \left(2\right).\]Модуль среднего ускорения найдем как:
\[\left\langle a\right\rangle =\frac{\Delta v}{\Delta t}=\frac{v\Delta l}{r\Delta t}\left(3\right).\]Величину мгновенного ускорения можно получить, перейдя к пределу при $\Delta t\to 0\ $ от $\left\langle a\right\rangle $:
\[a={\mathop{\lim }_{\Delta t\to 0} \left\langle a\right\rangle \ }={\mathop{\lim }_{\Delta t\to 0} \frac{v\Delta l}{r\Delta t}=\frac{v}{r}\ }\mathop{{\rm lim}}_{\Delta t\to 0}\frac{\Delta l}{\Delta t}=\frac{v}{r}v=\frac{v^2}{r}\left(4\right).\]Вектор среднего ускорения составляет с вектором скорости угол равный:
\[\beta =\frac{\pi +\alpha }{2}\left(5\right).\]При $\Delta t\to 0\ $ угол $\alpha \to 0.$ Получается, что вектор мгновенного ускорения составляет с вектором скорости угол $\frac{\pi }{2}$.
Мы получили, что материальная точка, равномерно движущаяся по окружности, имеет ускорение, направленное к центру траектории движения (перпендикулярное вектору скорости), его модуль равен скорости в квадрате, деленной на радиус окружности. Такое ускорение называют центростремительным или нормальным, обозначают его обычно ${\overline{a}}_n$.
\[a_n=\frac{v^2}{r}={\omega }^2r\ \left(6\right),\]где $\omega $ - угловая скорость движения материальной точки ($v=\omega \cdot r$).
Определение центростремительного ускорения
Центростремительное ускорение равно:
\[{\overline{a}}_n=\frac{v^2}{r^2}\overline{r\ }\left(7\right),\]где $e_r=\frac{\overline{r\ }}{r}$ - единичный вектор, направленный от центра кривизны траектории к рассматриваемой точке.
Впервые верные формулы для центростремительного ускорения были получены Х. Гюйгенсом.
Единицей измерения центростремительного ускорения в Международной системе единиц является метр, деленный на секунду в квадрате:
\[\left[a_n\right]=\frac{м}{с^2}.\]Примеры задач с решением
Задание. Диск вращается вокруг неподвижной оси. Закон изменения угла поворота радиуса диска задает уравнение: $\varphi =5t^2+7\ (рад)$. Чему равно центростремительное ускорение точки A диска, которая находится на расстоянии $r=$0,5 м от оси вращения к окончанию четвертой секунды от начала вращения?
Решение. Сделаем рисунок.
Угловую скорость вращения точки найдем как:
\[\omega =\frac{d\varphi }{dt}\ (1.2)\]уравнение изменения угла поворота в зависимости о времени:
\[\omega =\frac{d\left(5t^2+7\right)}{dt}=10t\ \left(1.3\right).\]В конце четвертой секунды угловая скорость равна:
\[\omega \left(t=4\right)=10\cdot 4=40\ \left(\frac{рад}{с}\right).\]Используя выражение (1.1) найдем величину центростремительного ускорения:
\[a_n={(40)}^2\cdot 0,5=800\ \left(\frac{м}{с^2}\right).\]Ответ. $a_n=800\frac{м}{с^2}$.
Задание. Движение материальной точки задается при помощи уравнения: $\overline{r}\left(t\right)=0,5\ (\overline{i}{\cos \left(\omega t\right)+\overline{j}{\sin (\omega t)\ }\ })$, где $\omega =2\ \frac{рад}{с}$. Какова величина нормального ускорения точки?
Решение. За основу решения задачи примем определение центростремительного ускорения в виде:
\[a_n=\frac{v^2}{R}\left(2.1\right).\]Из условий задачи видно, что траекторией движения точки является окружность. В параметрическом виде уравнение: $\overline{r}\left(t\right)=0,5\ (\overline{i}{\cos \left(\omega t\right)+\overline{j}{\sin (\omega t)\ }\ })$, где $\omega =2\ \frac{рад}{с}$ можно представить как:
\[\left\{ \begin{array}{c} x=0,5{\cos \left(2t\right);;\ } \\ y=0,5{\sin \left(2t\right).\ } \end{array} \right.\]Радиус траектории можно найти как:
\[R=\sqrt{x^2+y^2}=\sqrt{{(0,5{\cos (2t)\ })}^2+{(0,5{sin (2t))\ }}^2}=\sqrt{{\left(0,5\right)}^2(c{os}^2\left(2t\right)+{sin}^2(2t))}=0,5.\]Компоненты скорости равны:
\[v_x=\frac{dx}{dt}=-0,5\cdot 2{\sin \left(2t\right)\ }\left(2.2\right).\] \[v_y=\frac{dy}{dt}=0,5\cdot 2{\cos \left(2t\right)\ }\left(2.3\right).\]Получим модуль скорости:
\[v=\sqrt{v^2_x+v^2_y}=\sqrt{{{sin}^2 \left(2t\right)+{cos}^2(2t)\ }}=1\ \left(\frac{м}{с}\right)(2.4).\]Подставим величину скорости и радиус окружности в выражение (2.2), имеем:
\[a_n=\frac{1^2}{0,5}=2\left(\frac{м}{с^2}\right).\]Ответ. $a_n=2\frac{м}{с^2}$.
Читать дальше: сила тяги.










