Закон Паскаля для жидкостей и газов, теория и онлайн калькуляторы
Закон Паскаля для жидкостей и газов
Жидкости и газы передают давление, которое оказывается на них, по всем направлениям одинаково.
Данный закон был открыт в середине XIV века французским ученым Б. Паскалем и получил впоследствии его имя.
То, что жидкости и газы передают давление, объясняют большой подвижностью частиц, из которых они составлены, это существенным образом отличает их от твёрдых, тел, чьи частицы малоподвижны, и могут только совершать колебания около положений своего равновесия. Допустим, газ, находится в замкнутом сосуде с поршнем, его молекулы равномерно заполняют весь предоставленный ему объем. Передвинем поршень, уменьшив объем сосуда, слой газа, прилегающий к поршню, сожмется, молекулы газа будут располагаться плотнее, чем на некотором удалении от поршня. Но через некоторое время частицы газа, участвуя в хаотичном движении, перемешаются с другими частицами, плотность газа выровняется, но станет больше, чем до передвижения поршня. При этом количество ударов о дно и стенки сосуда возрастает, следовательно, давление поршня передается газом во всех направлениях одинаково и в каждой точке увеличивается на одну и ту же величину. Аналогичные рассуждения можно отнести к жидкости.
Формулировка закона Паскаля
Давление, производимое внешними силами на жидкость (газ), находящуюся в состоянии покоя, передается веществом во все стороны без изменения к любой точке жидкости (газа) и стенкам сосуда.
Закон Паскаля выполняется для несжимаемых и сжимаемых жидкостей и газов, если сжимаемостью пренебрегают. Этот закон - следствие закона сохранения энергии.
Гидростатическое давление жидкостей и газов
Жидкости и газы передают не только внешнее давление, но и давление, которое возникает благодаря существованию силы тяжести. Эта сила создает внутри жидкости (газа) давление, которое зависит от глубины погружения, при этом приложенные внешние силы увеличивают это давление в любой точке вещества на одну и ту же величину.
Давление, которое оказывает покоящаяся жидкость (газ), называют гидростатическим. Гидростатическое давление ($p$) на любой глубине внутри жидкости (газа) не зависит от формы сосуда, в котором она (он) находится и равно:
\[p=\rho gh\ \left(1\right),\]
где $h$ - высота столба жидкости (газа); $\rho $ - плотность вещества. Из формулы (1) для гидростатического давления следует, что во всех местах жидкости (газа), которые находятся на одной глубине, давление одно и то же. С увеличением глубины гидростатическое давление растет. Так, на глубине 10 км давление воды составляет приблизительно ${10}^8Па$.
Следствие закона Паскаля: давление в любой точке на одном горизонтальном уровне жидкости (газа), находящейся в состоянии равновесия имеет одну и ту же величину.
Примеры задач с решением
Пример 1
Задание. Даны три сосуда разной формы (рис.1). Площадь дна каждого сосуда равна $S$. В каком из сосудов давление одной и той же жидкости на дно наибольшее?
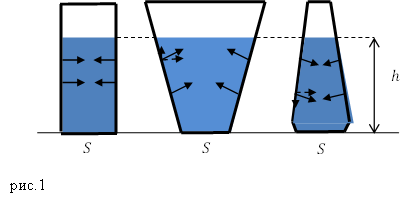
Решение. В данной задаче речь идет о гидростатическом парадоксе. Следствием закона Паскаля является то, что давление жидкости не зависит от формы сосуда, а определено высотой столба жидкости. Так как по условию задачи площадь дна каждого сосуда равна S, из рис.1 видим, что высота столбов жидкости одинакова, несмотря на разный вес жидкости, сила «весового» давления на дно во всех сосудах одинакова и равна весу жидкости в цилиндрическом сосуде. Объяснение этого парадокса заключено в том, что сила давления жидкости на наклонные стенки имеет вертикальную составляющую, которая направлена вниз в сужающемся к верху сосуде и направленную вверх в расширяющемся.
Пример 2
Задание. На рис.2 изображены два сообщающихся сосуда с жидкостью. Поперечное сечение одного из сосудов в $n\ $ раз меньше, чем второго. Сосуды закрыты поршнями. К малому поршню прикладывают силу $F_2.\ $Какой силой надо подействовать на большой поршень, чтобы система находилась в состоянии равновесия?
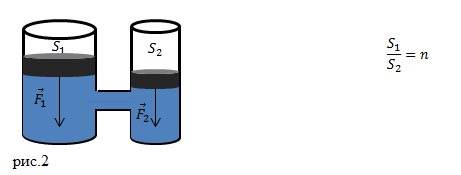
Решение. В задаче представлена схема гидравлического пресса, который работает на основе закона Паскаля. Давление, которое создает на жидкость первый поршень, равен:
\[p_1=\frac{F_1}{S_1}\left(2.1\right).\]
Второй поршень оказывает на жидкость давление:
\[p_2=\frac{F_2}{S_2}\left(2.2\right).\]
Если система находится в равновесии, $p_1$ и $p_2$ равны, запишем:
\[\frac{F_1}{S_1}=\frac{F_2}{S_2}\left(2.3\right).\]
Найдем модуль силы, приложенной к большому поршню:
\[F_1=F_2\frac{S_1}{S_2}=nF_{2.}\]
Ответ. $F_1=nF_{2}$
Читать дальше: линейная скорость вращения.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 460 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!












