Натуральное число, единственными делителями которого является лишь оно само и единица, называется простым числом.
Составные числа - числа, которые имеют другие делители, кроме единицы и самого себя.
Содержание:
Определение
Натуральное число, единственными делителями которого является лишь оно само и единица, называется простым числом.
Составные числа - числа, которые имеют другие делители, кроме единицы и самого себя.
Пример
Число 5 - простое число, так как 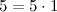 , то есть единственными
делителями пятерки есть само это число 5 и единица. Число 6 составное, так как оно кратно следующим числам: 1, 2, 3, 6.
, то есть единственными
делителями пятерки есть само это число 5 и единица. Число 6 составное, так как оно кратно следующим числам: 1, 2, 3, 6.
Натуральное число 1 не есть ни простым, ни составным числом.
Представление натурального числа 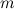 в виде
произведения двух натуральных чисел
в виде
произведения двух натуральных чисел 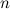 и
и 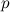 :
:
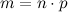 называется разложением на множители.
называется разложением на множители.
При этом считается, что если число 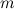 простое,
то оно раскладывается на множители, которые состоят из единственного числа
простое,
то оно раскладывается на множители, которые состоят из единственного числа 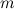 .
.
Пример
Разложение составного числа 6 на множители имеет вид: 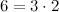 ;
разложение простого числа 5 на множители:
;
разложение простого числа 5 на множители: 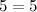 , а
не
, а
не 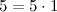 .
.
Пусть натуральное число 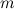 составное, то есть
составное, то есть
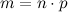 ,
,
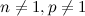 . При этом возможны следующие случаи:
. При этом возможны следующие случаи:
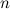 и
и
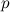 простые, то
число
простые, то
число 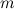 можно записать в виде произведения
двух простых чисел
можно записать в виде произведения
двух простых чисел 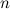 и
и
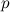 .
.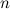 и
и
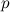 составное, то это составное число
(или оба этих составных числа
составное, то это составное число
(или оба этих составных числа 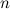 и
и
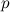 ) раскладывают в произведение еще
меньших натуральных чисел, для которых возможны эти самые случаи. Так как множество чисел, меньших
) раскладывают в произведение еще
меньших натуральных чисел, для которых возможны эти самые случаи. Так как множество чисел, меньших
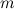 , конечно, то указанный процесс
разложения закончится после конечного числа шагов. В результате получим разложение числа
, конечно, то указанный процесс
разложения закончится после конечного числа шагов. В результате получим разложение числа
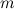 на множители, каждый из которых является
простым числом.
на множители, каждый из которых является
простым числом.Представление натурального числа 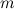 в виде
произведения простых чисел называется разложением на простые множители.
в виде
произведения простых чисел называется разложением на простые множители.
Теорема
Каждое натуральное число, отличное от 1, можно единственным способом разложить на простые множители, причем
разложения 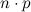 и
и
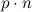 считаются тождественными (
считаются тождественными (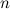 и
и
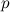 - простые числа).
- простые числа).
Объединяя в разложении числа 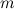 одинаковые простые
сомножители, получаем каноническое разложение числа
одинаковые простые
сомножители, получаем каноническое разложение числа 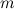 :
:
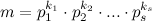 , где
, где
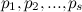 - разные простые числа,
- разные простые числа,
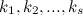 - натуральные числа.
- натуральные числа.
Пример
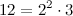
Читать следующую тему: взаимно простые числа.