Движение под углом к горизонту, теория и онлайн калькуляторы
Движение под углом к горизонту
Пусть некоторое тело бросили под углом $\alpha \ $к горизонту, с начальной скоростью ${\overline{v}}_0$. Введем некоторые допущения: Тело будем рассматривать как материальную точку. Сопротивление воздуха учитывать не будем.
Постанова задачи. Начальные условия движения под углом к горизонту
Тело брошено с высоты ${y=h}_0$; $x_0=0$.
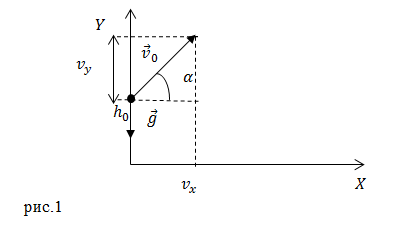
Начальные условия при рассматриваемом движении точки таковы:
\[при\ t=0\ c\left\{ \begin{array}{c}
x_0=0, \\
y_0=h, \\
v_{0x}=v_0{\cos \alpha ,\ } \\
v_{0y}=v_0{\sin \alpha .\ } \end{array}
\right.(1)\]
Вектор ускорения при движении в поле тяжести Земли считают постоянной величиной:
\[\overline{a}=\overline{g}\left(2\right),\]
где $\overline{g}$ направлен вертикально вниз и равен по величине приблизительно 9,8 $\frac{м}{с^2}.$ Проекция ускорения на ось X равна нулю, а на ось Y равна $a_y=g.$
Уравнение для скорости движения под углом к горизонту
Скорость движения такого тела определяют как:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(3\right),\]
где ${\overline{v}}_0$ - скорость тела в момент броска. Формулу (2) можно рассматривать как результат сложения скоростей двух независимых движений по прямым линиям, в которых участвует тело, брошенное под углом к горизонту. Это равномерное перемещение с постоянной скоростью ${\overline{v}}_0$ в горизонтальном направлении и равноускоренного движения с ускорением $\overline{g}$ без начальной скорости в направлении вектора ускорения свободного падения.
Проектируя выражение (3) на оси координат получаем:
\[\left\{ \begin{array}{c}
v_x=v_0{\cos \alpha ,\ } \\
v_y=v_0{\sin \alpha -gt\ } \end{array}
\left(4\right).\right.\]
Траектория движения тела
Не смотря на то, что каждое отдельное движение тела происходит по прямой, результирующей траекторией является парабола, лежащая в плоскости в которой находятся векторы ${\overline{v}}_0$ и $\overline{g}$.
Уравнение перемещения при равнопеременном движении при$\overline{a}=\overline{g}$:
\[\overline{s}\left(t\right)={\overline{s}}_0+{\overline{v}}_0t+\frac{\overline{g}t^2}{2}(5),\]
где ${\overline{s}}_0$ - смещение тела в начальный момент времени. В нашем случае $s_0=h$. Уравнения для координат точки, брошенной под углом к горизонту из уравнения для перемещения:
\[\left\{ \begin{array}{c}
x=v_0{\cos \left(\alpha \right)\cdot t,\ } \\
y={h+v}_0{\sin \left(\alpha \right)\cdot t-\frac{gt^2}{2}\ } \end{array}
\left(6\right).\right.\]
Из систем уравнений (5) и (6) траектория движения материальной точки получается, задана уравнением:
\[y=h+x\ tg\ \alpha -\frac{gx^2}{2v^2_0{cos}^2\alpha }\left(7\right).\]
По форме уравнения (7) видно, что траекторией движения является парабола.
Время подъема и полета тела
Время подъема тела при рассматриваемом движении легко определить из системы уравнений (4). В точке максимального подъема вектор скорости точки параллелен оси X, значит $v_y=0$, время подъема ($t_p$) равно:
\[t_p=\frac{v_0{\sin \alpha \ }}{g}\left(8\right).\]
Время, которое тело пребывало в воздухе (время полета($t_{pol}$)) определяют из второго уравнения системы (6), приравнивая координату $y$ к нулю, получают:
\[t_{pol}=\frac{v_0{\sin \alpha +\sqrt{v^2_0{sin}^2\alpha +2gh}\ }}{g}\left(9\right).\]
Дальность полета и высота подъема
Для того чтобы найти горизонтальную дальность полета тела ($s$) при заданных нами условиях в уравнение координаты $x$ системы уравнений (6) подставим время полета ($t_{pol}$) (9). При $h=0,$ дальность полета равна:
\[s=\frac{v^2_0{\sin \left(2\alpha \right)\ }}{g}\left(10\right).\]
Максимальную высоту подъема тела ($h_{max}$) находят из второго уравнения системы (6), подставляя в него время подъема ($t_p$) (8):
\[h_{max}=h+\frac{{v_0}^2{{sin}^2 б\ }}{2g}\left(11\right).\]
Выражение (11) показывает, что максимальная высота подъема тела прямо пропорциональна квадрату скорости бросания и увеличивается при росте угла бросания.
Примеры задач на движение под углом к горизонту
Пример 1
Задание. Маленький шарик лежит на краю горизонтальной поверхности, которая находится на высоте $h$ над уровнем Земли. Ему сообщают начальную скорость направленную горизонтально. По какой траектории будет двигаться шарик? Сопротивление воздуха не учитывайте.
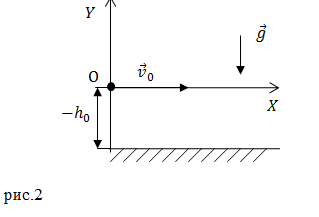
Решение. Начало координат системы отсчета поместим в точку начала падения шарика (рис.2). Основой для решения задачи является уравнение:
\[\overline{s}\left(t\right)={\overline{s}}_0+{\overline{v}}_0t+\frac{\overline{g}t^2}{2}\left(1.1\right)\]
В проекции на оси координат векторное уравнение даст два скалярных. Так из уравнения (1.1) получаем:
\[\left\{ \begin{array}{c}
X:\ x=v_0t \\
Y:y=-\frac{gt^2}{2} \end{array}
\right.\left(1.2\right).\]
Для того чтобы определить какой будет траектория движения шарика нам нужно получить функцию связывающую координаты $y$ и $x$ ($y=y(x)$). Для этого выразим из первого уравнения системы (1.2) время и подставим его во второе уравнение этой же системы:
\[t=\frac{x}{v_0};;y=-\frac{gt^2}{2}=-\ \frac{g}{2}{\left(\frac{x}{v_0}\right)}^2=-\frac{g}{2v^2_0}x^2.\]
Мы получили функцию:
\[y=-\frac{g}{2v^2_0}x^2=-kx^2(1.3).\]
Уравнение (1.3) - это уравнение параболы. Учитывая, что $t>0$, получим ветвь параболы, вершина в точке бросания.
Ответ. Ветвь параболы.
Пример 2
Задание. Как зависит дальность полета тела, брошенного под углом к горизонту от величины угла бросания? Как влияет сопротивление воздуха на дальность полета тела при его движении под углом к горизонту?
Решение. Будем считать, что тело бросили из начала отсчета ($h=0$). Тогда, дальность полета тела при бросании его под углом к горизонту $\alpha $ равна:
\[s=\frac{v^2_0{\sin \left(2\alpha \right)\ }}{g}\left(2.1\right).\]
Из выражения (2.1) следует, что при заданной скорости бросания дальность полета при увеличении угла$\ \ \alpha \ $растет. Становится максимальной при $\alpha =\frac{\pi }{4}$. Если далее увеличивать угол бросания, то дальность полета тела станет уменьшаться при $\alpha =\frac{\pi }{2}$, тело упадет в точку бросания.
Если учитывать сопротивление воздуха, то дальность полета тела уменьшится в несколько раз.
Читать дальше: движение тела, брошенного под углом к горизонту.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 466 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!












