Равноускоренное движение, теория и онлайн калькуляторы
Равноускоренное движение
Прямолинейное равнопеременное движение
Определение
Равнопеременным движением материальной точки называют движение, при котором его мгновенная скорость ($\overline{v}$) -
это линейная функция времени:
\[\overline{v}={\overline{v}}_0+\overline{a}t\left(1\right),\]
где ${\overline{v}}_0=const$ - начальная скорость точки (Под начальной скоростью понимают скорость точки в момент начала наблюдения. Этот момент времени может не совпадать с началом движения); $\overline{a}=const$ - ускорение точки; $t$ - время.
Определим смысл величины $a$ в формуле (1). Из определения среднего ускорения ($\left\langle a\right\rangle $):
\[\left\langle \overline{a}\right\rangle =\frac{{\overline{v}}_2-{\overline{v}}_1}{t_2-t_1}=\frac{{\overline{v}}_0+{\overline{a}t}_2-{\overline{v}}_0-{\overline{a}t}_1}{t_2-t_1}=\frac{\overline{a}(t_2-t_1)}{t_2-t_1}=\overline{a}\left(2\right).\]
Мгновенное ускорение при равнопеременном движении совпадает со средним ускорением. Поэтому равнопеременным движением называют движение с постоянным ускорением.
Если направления вектора ускорения и скорости при равнопеременном движении совпадают, то такое движение называют равноускоренным. Скорость материальной точки в таком движении увеличивается за равные промежутки времени на одну и ту же величину.
График скорости при равноускоренном движении
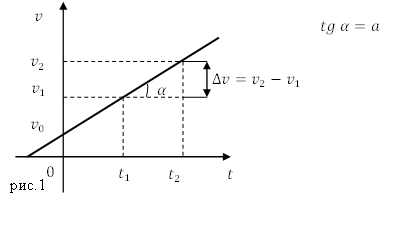
Для построения графика скорости на оси абсцисс отложим значения времени, на оси ординат - соответствующие им значения мгновенной скорости. Линия, которая соединяет полученные точки будет графиком скорости. Графиком скорости при равноускоренном движении является прямая, которая отсекает на оси ординат величину начальной скорости (рис.1). Тангенс угла наклона прямой равен модулю ускорения:
\[tg\ \alpha =\frac{v_2-v_1}{t_2-t_1}=a\left(3\right).\]
При равноускоренном движении график скорости образует острый угол с осью абсцисс ($\alpha <\frac{\pi }{2}$).
Путь, перемещение и средняя скорость при равноускоренном движении
Координата материальной точки движущейся с постоянным ускорением, является квадратичной функцией времени. Пусть точка движется по оси X, тогда при равноускоренном движении:
\[x=x_0+v_0t+\frac{at^2}{2};;x-x_0=\frac{v^2-v^2_0}{2a}\left(4\right),\]
где $x_0$ - координата точки при $t=0\ $с.
Путь, пройденный точкой при равноускоренном движении равен:
\[s=s_0+v_0t+\frac{at^2}{2}\left(5\right),\]
$s_0$ - путь, пройденный точкой до начала отсчета времени.
График пройденного пути - парабола.
Перемещение ($\overline{s}$) материальной точки при равноускоренном движении определяет формула:
\[\overline{s}={\overline{s}}_0+{\overline{v}}_0t+\frac{\overline{a}t^2}{2}\left(6\right),\]
где ${\overline{s}}_0$ при $t=0$ c.
Модуль средней скорости при равнопеременном движении материальной точки равен:
\[\left\langle v\right\rangle =\frac{v_1+v_2}{2}\left(7\right).\]
Примеры задач с решением
Пример 1
Задание. На рис.2 изображены графики $v_x(t)$ двух прямолинейных движений. Сравните для этих движений 1) модули ускорений; 2) пути, которые пройдены точкой за время $\tau $ от начала первого движения.
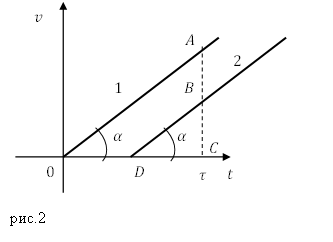
Решение. 1) На графике представлены функции $v(t)$ для двух равноускоренных движений, так как мы видим, что скорость изображена прямой линией, отображающей линейную связь скорости и времени. Угол наклона прямой по отношению к оси абсцисс острый, следовательно, движения равноускоренные. Угла наклона равные, значит, равны и их тангенсы, а мы знаем, что:
\[a=tg\ \alpha \left(1.1\right).\]
Получаем, что:
\[a_1=a_2.\]
2) Путь пройденный точкой равен:
\[s=\int\limits^{t_2}_{t_1}{v\left(t\right)dt}\left(1.2\right).\]
Выражение (1.2) означает, что путь материальной точки численно равен площади криволинейной трапеции, которая ограничена внизу осью абсцисс, справа и слева значением мгновенной скорости в моменты времени $t_1$ и $t_2$, вверху графиком скорости. В нашей задаче для сравнения пути следует сравнить площади треугольников OAC и DBC. Очевидно, что:
\[S_{OAC}>S_{DBC}\to s_1>s_2.\]
Ответ. 1) $a_1=a_2.$ 2) $s_1>s_2$
Пример 2
Задание. На рис. 3 (а,б) даны графики двух прямолинейных равноускоренных движений. Сравните 1) конечные скорости этих движений; 2) ускорения. Начальная скорость обоих движений равна нулю.
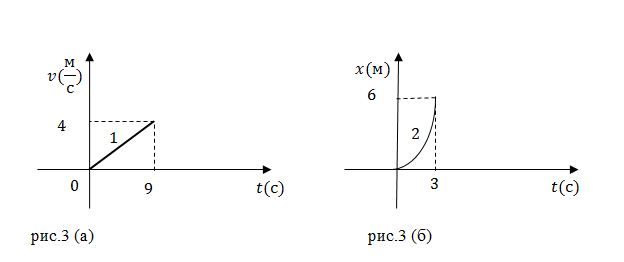
Решение. Рассмотрим рисунок 3 (а). Конечная скорость движения при равноускоренном движении для первого графика из рис. 3 (а) равна: $v_1\left(t=9c\right)=4\ \frac{м}{с}$ . Скорость с ускорением при равноускоренном движении по прямой равна:
\[v=v_0+at=at\ \left(2.1\right),\]
где $v_0=0\frac{м}{с}$ по условию задачи. Из (2.1) ускорение точки равно:
\[a=\frac{v}{t}\left(2.2\right).\]
Рассмотрим конечный момент времени ($t=9$с);$\ v=4\ \frac{м}{с}$ :
\[a_1=\frac{4}{9}\ \left(\frac{м}{с^2}\right).\]
Рассмотрим рис. 3 (б). Координата материальной точки связана со временем при равноускоренном движении как:
\[x=x_0+v_0t+\frac{at^2}{2}\left(2.3\right).\]
где из рис.3 (б) видно, что $x_0=0\ м;;$ по условию задачи $v_0=0\ \frac{м}{с}$, тогда выражение (2.3) преобразуется к виду:
\[x=\frac{at^2}{2}\left(2.4\right).\]
Выразим ускорение точки:
\[a=\frac{2x}{t^2}\left(2.5\right).\]
Их графика имеем, что $x\left(t=3\right)=6$, следовательно:
\[a_2=\frac{2\cdot 6}{3^2}=\frac{4}{3}\left(\frac{м}{с^2}\right).\]
Найдем скорость материальной точки для графика рис. 3(б), используя формулу (2.1):
\[v_2=a_2t_2=\frac{4}{3}\cdot 3=4\left(\frac{м}{с}\right).\]
Ответ. 1) Конечные скорости движений равны. 2) $a_1$ меньше $a_2$
Читать дальше: сила натяжения нити.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 451 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!













