Пусть в некоторой системе тел действуют только консервативные силы. Сумму потенциальной ($E_p$) и кинетической ($E_k$) энергии называют полной механической энергией ($W$) системы:
\[W=E_p+E_k\ \left(1\right).\]Закон сохранения энергии
Механическая энергия и ее сохранение
Определение
Пусть наша консервативная система замкнута, значит, в ней действуют только внутренние силы. Работа ($A$) внутренних сил равна изменению кинетической энергии:
\[A=E_{k2}-E_{k1}\left(2\right).\]Кроме того работа равна изменению потенциальной энергии системы:
\[A=E_{p1}-E_{p2}\left(3\right).\]Если равны левые части выражений (2) и (3), то приравняем их правые части:
\[E_{k2}-E_{k1}=E_{p1}-E_{p2}\to E_{k2}+E_{p2}=E_{k1}+E_{p1}\left(4\right).\]Выражение (4) означает, что механическая энергия замкнутой консервативной системы сохраняется:
\[W=E_p+E_k=const\ \left(5\right).\] (5) - закон сохранения механической энергии в механике Ньютона.Закон сохранения энергии в термодинамике
Энергию тела можно изменить, совершая над ним работу. Работа внешней силы есть мера полной энергии тела. Например, некоторая сила деформирует тело. При этом изменяются расстояния между частицами тела, что ведет к изменению внутренней энергии тела. Кроме упругой деформации происходит изменение температуры тела, что тоже говорит об изменении внутренней энергии тела. При деформации совершается работа, она является мерой изменения внутренней энергии тела. Изменение внутренней энергии тела может происходить под действием силы трения, так как трение сопровождается изменением температуры контактирующих поверхностей тел. Работа силы трения может служить мерой измерения внутренней энергии.
Кроме работы существует еще один способ изменения энергии тела. Это теплопередача. Процесс передачи энергии от одного тела (с более высокой температурой) к другому телу (с более низкой температурой) без совершения работы называют теплообменом. Фактически изменение внутренней энергии происходит под действием молекулярных соударений. У нагретого тела частицы движутся с большими скоростями, чем у холодного. При контакте тел происходят упругие соударения молекул. Быстрые частицы передают часть своей кинетической энергии медленным частицам.
Теплообмен может реализовываться за счет видимых и невидимых излучений. Процесс передачи энергии при помощи электромагнитных волн называют теплообменом с помощью излучения. Теплообмен с помощью излучения возможен в вакууме. Мерой изменения энергии тела при теплообмене служит количество теплоты ($Q$).
Количеством теплоты называют энергию, которая передается в процессе теплообмена. Количество теплоты, которое получает система ($\Delta Q$), расходуется на изменение внутренней энергии ($\Delta U$) этого тела (системы) и на выполнение работы этим телом (системой) над внешними силами:
\[\Delta Q=A+\Delta U\ \left(6\right).\]Выражение (6) называют первым началом термодинамики в интегральном виде. Это одна из форм представления закона сохранения энергии.
Общая формулировка закона сохранения энергии
Пусть мы имеем систему, которая не взаимодействует с окружающим ее миром механическим путем (система замкнута), у нее нет теплообмена (система адиабатически изолирована). Тогда мы можем сказать, что работа системы над внешними силами равна нулю ($A=0$). Из адиабатической изоляции следует, что $\Delta Q=0$. Тогда из первого начала термодинамики следует, что изменение внутренней энергии системы равно нулю ($\Delta U=0$).
Полная энергия замкнутой и адиабатически изолированной системы является постоянной величиной. Это наиболее общая формулировка закона сохранения энергии.
Закон сохранения энергии не требует, чтобы энергия каждого тела, которое входит в систему сохранялась. Между телами внутри системы может реализовываться взаимодействие и механическое и теплообмен.
Примеры задач с решением
Пример 1
Задание. Какова минимальная высота, с которой необходимо скатиться тележке по желобу, который переходит в петлю радиусом R, чтобы она не оторвалась в верхней точке петли?
Решение. Сделаем рисунок
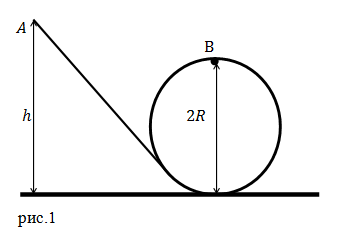
Тело в точке A обладает потенциальной энергией равной:
\[E_{p1}=mgh\ \left(1.1\right).\]При движении вниз в точке B эта потенциальная энергия переходит в кинетическую энергию:
\[E_k=\frac{mv^2}{2}\left(1.2\right),\]и потенциальную энергию:
\[E_{p2}=mgh'=mg2R\ \left(1.3\right).\]Так как трение не учитываем, считаем систему замкнутой и консервативной, то выполняется закон сохранения механической энергии:
\[mgh=\frac{mv^2}{2}+2mgR\ \left(1.4\right).\]Рассмотрим силы, действующие на тело, которое движется по окружности. Получим по второму закону Ньютона, что:
\[mg=ma=m\frac{v^2}{R}\to v^2=gR\ \left(1.5\right).\]Подставим полученную скорость (1.5) в формулу (1.4), найдем искомую высоту:
\[gh=\frac{gR}{2}+2gR\to h=\frac{4R+R}{2}=\frac{5}{2}R.\]Ответ. $h=\frac{5}{2}R.$
Пример 2
Задание. Газ массой $m$ сжимают изотермически при температуре T от давления $p_1$ до давления $p_2$. Каково изменение внутренней энергии газа, работа сжатия и количество выделившейся теплоты? Газ считать идеальным. Молярная масса газа равна $\mu $.
Решение. При изотермическом процессе внутренняя энергия газа не изменяется, следовательно:
\[\Delta U=0\ \left(2.1\right).\]Работа газа равна:
\[A=\int\limits^{V_2}_{V_1}{pdV\ \left(2.2\right).}\]Так как газ идеальный воспользуемся уравнением Менделеева- Клапейрона и законом Бойля -Мариотта для изотермического процесса:
\[pV=\frac{m}{\mu }RT;;p_1V_1=\ p_2V_2(2.3)\]из него выразим давление и подставим в формулу работы:
\[A=\int\limits^{V_2}_{V_1}{\frac{m}{\mu }RT\ \frac{dV}{V}=\ \frac{m}{\mu }RTln\ \left(\frac{V_2}{V_1}\right)=\frac{m}{\mu }RTln\ \left(\frac{p_1}{p_2}\right)\left(2.2\right).}\]Следует учесть, что по условию работу совершают над газом, значит, она будет отрицательной.
В соответствии с первым началом термодинамики:
\[\Delta Q=A=\frac{m}{\mu }RTln\ \left(\frac{p_1}{p_2}\right)\ \left(2.3\right).\]Работу совершают над газом, а теплота будет выделяться.
Ответ. $A=-\frac{m}{\mu }RTln\ \left(\frac{p_1}{p_2}\right);;\ \Delta Q=\frac{m}{\mu }RTln\ \left(\frac{p_1}{p_2}\right).$
Читать дальше: первый закон Ньютона.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Статьи по теме
Поможем выполнить
любую работу
