Период колебания пружинного маятника, теория и онлайн калькуляторы
Период колебания пружинного маятника
Рассмотрим простейшую систему, в которой возможна реализация механических колебаний. Допустим, что на упругой пружине, жесткость которой равна $k,$ подвешен груз массой $m$. Груз движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе. Массу пружины считаем малой в сравнении с массой груза.
Уравнение движения груза при таких колебаниях имеет вид:
\[\ddot{x}+{\omega }^2_0x=0\left(1\right),\]
где ${\omega }^2_0=\frac{k}{m}$ - циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:
\[x=A{\cos \left({\omega }_0t+\varphi \right)=B{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(2\right),\]
где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ и $B$ - амплитуда колебаний; ${(\omega }_0t+\varphi )$ - фаза колебаний; $\varphi $ и ${\varphi }_1$ - начальные фазы колебаний.
Частота и период колебаний пружинного маятника
Косинус (синус) - периодическая функция, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называют
периодом колебаний. Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($\nu $):
\[T=\frac{1}{\nu }\left(3\right).\]
Период связан с циклической частотой колебаний как:
\[T=\frac{2\pi }{{\omega }_0}\left(4\right).\]
Зная, что для пружинного маятника ${\omega }_0=\sqrt{\frac{k}{m}}$, период колебаний его определим как:
\[T=2\pi \sqrt{\frac{m}{k}}\ \left(5\right).\]
Из выражения (5) мы видим, что период колебаний пружинного маятника зависит от массы груза, находящегося на пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Такое свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, при этом возникает зависимость колебаний от амплитуды. Отметим, что формула (5) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Единицей измерения периода являются единицы времени, в Международной системе единиц это секунды:
\[\left[T\right]=с.\]
Примеры задач на период колебания пружинного маятника
Пример 1
Задание. К упругой пружине прикрепили небольшой груз, при этом пружина растянулась на $\Delta x$=0,09 м. Каким будет период колебаний данного пружинного маятника, если его вывести из равновесия?
Решение. Сделаем рисунок.
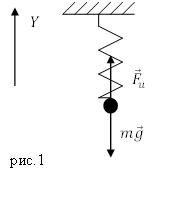
Рассмотрим состояние равновесия пружинного маятника. Груз прикрепили, после этого пружина растянулась на величину $\Delta x$, маятник находится в состоянии равновесия. На груз действуют две силы: сила тяжести и сила упругости. Запишем второй закон Ньютона для состояния равновесия груза:
\[m\overline{g}+{\overline{F}}_u=0\ \left(1.1\right).\]
Запишем проекцию уравнения (1.1) на ось Y:
\[mg=F_u\left(1.2\right).\]
Так как груз по условию задачи небольшой, пружина растянулась не сильно, следовательно выполняется закон Гука, величину силы упругости найдем как:
\[F_u=k\Delta x\ \left(1.3\right).\]
Используя выражения (1.2) и (1.3) найдем отношение $\frac{m}{k}$:
\[mg=k\Delta x\to \frac{m}{k}=\frac{\Delta x\ }{g}\left(1.4\right).\]
Период колебаний пружинного маятника при малых колебаниях можно найти, используя выражение:
\[T=2\pi \sqrt{\frac{m}{k}}\ \left(1.5\right).\]
Заменяя отношение массы груза к жесткости пружины на правую часть выражения (1.4), получим:
\[T=2\pi \sqrt{\frac{\Delta x\ }{g}.}\]
Вычислим период колебаний нашего маятника, если $g=9,8\ \frac{м}{с^2}$:
\[T=2\pi \sqrt{\frac{0,09\ \ }{9,8}\ \approx 0,6\ (с)}\]
Ответ. $T$=0,6 с
Пример 2
Задание. Две пружины с жесткостями $k_1$ и $k_2$ соединены последовательно (рис.2), к концу второй пружины присоединен груз массы $m$, Каков период колебаний данного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука.
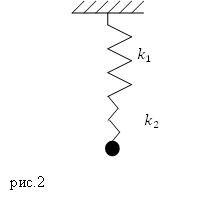
Решение.Период колебаний пружинного маятника равен:
\[T=2\pi \sqrt{\frac{m}{k}}\ \left(2.1\right).\]
Если две пружины соединены последовательно, то их результирующая жесткость ($k$) находится как:
\[\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}\to k=\frac{k_1k_2}{k_1{+k}_2}\left(2.2\right).\]
Вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:
\[T=2\pi \sqrt{\frac{m(k_1{+k}_2)}{k_1k_2}}.\]
Ответ. $T=2\pi \sqrt{\frac{m(k_1{+k}_2)}{k_1k_2}}$
Читать дальше: плечо силы.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 463 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!












