Закон всемирного тяготения, теория и онлайн калькуляторы
Закон всемирного тяготения
К началу XVII века гелиоцентрическая система мира была признана большинством ученых. Однако в то время не были понятны причины и законы, по которым планеты движутся.
И. Кеплер обработал результаты множества своих наблюдений и своего коллеги Т. Браге, сформулировал законы перемещения планет вокруг Солнца. Стало понятно, что для объяснения законов Кеплера, следует определить, какие силы действуют на планеты. Но Кеплеру и его современникам не удалось это выполнить. Задачу решил И. Ньютон.
Приблизительно, можно считать, что планеты перемещаются равномерно по орбитам, близким к окружностям. При таком виде движения материальной точки у нее имеется центростремительное ускорение, которое направлено к центру орбиты (для планеты, центростремительной ускорение направлено к Солнцу). Из второго закона Ньютона следует, что на планету, действует некоторая сила, которая порождает нормальное ускорение. Получается, что Солнце действует на каждую планету с силой, направленной к его центру. В соответствии с третьим законом Ньютона, планета действует на Солнце с силой, равной по величине предыдущей силе, но имеющей противоположное направление.
Закон всемирного тяготения
Мы знаем, что Луна совершает вращение вокруг Земли. Луна притягивает Землю, Земля притягивает Луну. И. Ньютон предположил, что
сила тяжести, с которой Земля притягивает все тела около своей поверхности, и сила с которой она притягивает Луну, имеют одно происхождение.
Ньютон сравнил ускорение свободного падения ($g=9,81\ \frac{м}{с^{2\ }}$ около поверхности Земли) и центростремительное ускорение ($a_n$),
которое имеет Луна при движении по своей орбите. Ньютон получил, что нормальное ускорение Луны равно $a_n=2,72\cdot {10}^{-3}\frac{м}{с^2}$.
Расхождение в величинах Ньютон пояснил тем, что сила тяготения убывает с ростом расстояния между притягивающимися телами. Ускорение, вызванное силой тяготения, убывает обратно пропорционально квадрату расстояния ($r$) между телами:
\[a_n=\frac{K}{r^2}\left(1\right),\]
где $K=const$.
Формулировка закона всемирного тяготения
Анализ нормального ускорения Луны при ее движении около Земли позволили И. Ньютону сделать вывод о том, что все тела в природе притягиваются с некоторыми силами, которые называются силами тяготения.
Допустим, что у нас имеются два тела, массы которых равны $m_1$ и $m_2$. Находятся они на расстоянии $r$ друг от друга. Эти тела взаимодействуют друг с другом с силами:
\[\ F_1=m_1a_1и\ F_2=m_2a_2\left(2\right)\]
По третьему закону Ньютона имеем:
\[\left|F_1\right|=\left|F_2\right|\left(3\right).\]
Принимая во внимание выражение (1), получаем:
\[m_1a_1=m_1\frac{K_1}{r^2}=m_2a_2=m_2\frac{K_2}{r^2}\ \left(4\right).\]
Выражение (4) будет выполняться, если $K_1=\gamma m_2,$ а $K_2=\gamma m_1,$ где $\gamma $ =const. То есть, мы получили, что:
\[F=m_1a_1=\gamma \frac{m_1m_2}{r^2}\left(5\right).\]
Формула (5) - математическое выражение закона всемирного тяготения: Сила тяготения между двумя материальными точками прямо пропорциональная их массам и обратно пропорциональная квадрату расстояния между ними.
Для точного расчёта силы взаимного притяжения формула (5) может быть применена только в том случае, если телами являются однородные шары, массы которых равны $m_{1\ }и\ m_2$, а $r$ - расстояние между их центрами.
Гравитационная постоянная
Коэффициент $\gamma $ называют гравитационной постоянной. В Международной системе единиц (система СИ) она равна $\gamma \approx 6,67\cdot {10}^{-11}\frac{м^3}{с^2\cdot кг}.\ $ Гравитационная постоянная численно равна силе взаимодействия материальных точек, имеющих массы по одному килограмму, расположенный на расстоянии в один метр. Гравитационная постоянная находится экспериментально.
Одним из первых эксперимент по измерению силы тяготения в лабораторных условиях поставил Кавендиш. Так была определена гравитационная постоянная.
Примеры задач с решением
Пример
Задание. В чем состоит суть опыта Кавендиша по измерению силы гравитации?
Решение. Сделаем рисунок.
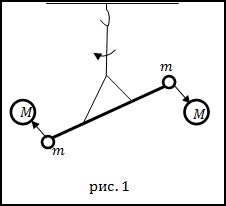
Для проведения эксперимента Кавендиш использовал крутильные весы (рис.1). На тонкой кварцевой нити подвешивался легкий стержень.
На нити жестко закреплялось маленькое зеркало. Луч света попадал на зеркало, отражался от него и падал на шкалу. Если стержень
поворачивался, то луч перемещался по шкале. Так отмечался угол закручивания нити. На концах стержня были закреплены два шарика из свинца,
каждый массой $m$. К этим шарикам подносили два симметрично расположенных свинцовых шарика массами $M$. Нить закручивалась до момента,
когда сила упругости деформированной нити не уравновешивает силу гравитационного взаимодействия между шарами. Сила взаимодействия измерялась
по углу закручивания нити. Зная массы шаров и расстояние между их центрами, вычислялась гравитационная постоянная.
Пример 2
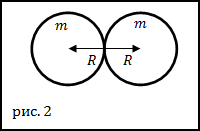
Задание. Два одинаковых однородных железных шара касаются друг друга (рис.2). Радиус каждого шара равен $R=0,1$ м. Какова сила гравитации, действующая между этими шарами?
Решение. Сделаем рисунок.
Основой для решения задачи служит закон всемирного тяготения:
\[F=\gamma \frac{m_1m_2}{r^2}\ \left(2.1\right),\]
где $m_1=m_2=m$ - массы каждого из шаров, тогда закон гравитации запишем в виде:
\[F=\gamma \frac{m^2}{r^2}\left(2.2\right).\]
Расстояние между центрами шаров (рис.2) равно: $r=2R.$ Массы шаров найдем как:
\[m=\rho \frac{4}{3}\pi R^3\left(2.3\right).\]
Формулу (2.2) преобразуем так:
\[F=\gamma \frac{{(\rho \frac{4}{3}\pi R^3)}^2}{{(2R)}^2}=\frac{\gamma {\rho }^2{\pi }^2R^4}{9}.\]
Для вычисления силы гравитации, найдем в справочниках плотность железа ($\rho =7800\ \frac{кг}{м^3}$). Гравитационная постоянная равна: $\gamma =6,67\cdot {10}^{-11}\frac{м^3}{с^2\cdot кг}.$ Проведем вычисления:
\[F=\frac{4\cdot 6,67\cdot {10}^{-11}{(7800\cdot \pi \cdot {\left({10}^{-1}\right)}^2)}^2}{9}=1,78\cdot {10}^{-6}\left(Н\right).\]
Ответ. $F=1,78\cdot {10}^{-6}$Н
Читать дальше: закон Гука.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 472 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!












