Единицы измерения момента инерции, теория и онлайн калькуляторы
Единицы измерения момента инерции
Определение
Моментом инерции тела, совершающего вращательные движения вокруг некоторой оси называют физическую величину ($J$), равную:
\[J=\sum\limits^k_{i=1}{{\Delta m}_ir^2_i\left(1\right),}\]
где ${\Delta m}_i$ - масса $i$ - той материальной точки, которая является частью
рассматриваемого тела; $r^2_i$ - расстояние в квадрате от $i$- той материальной точки до оси вращения тела.
Число материальных точек, на которое разбито тело равно в нашем случае $k$. Если тело непрерывно и однородно, то:
\[J=\int\limits_m{r^2dm=\int\limits_V{r^2}\rho dV=\rho \int\limits_V{r^2}dV\left(2\right),}\]
где $r$ - функция положения материальной точки в пространстве; $\rho $ - плотность тела; $dV$ -объем элемента тела.
Килограмм, умноженный на метр в квадрате - единица измерения момента инерции в системе СИ
Проще всего единицу измерения момента инерции тела определить, если рассмотреть материальную точку, вращающуюся вокруг неподвижной оси:
\[J=mr^2\left(3\right),\]
где $m$ - масса материальной точки; $r$ - расстояние от нее до оси вращения.
Из выражения (3) очевидно, что:
\[\left[J\right]=кг\cdot м^2.\]
Килограмм - метр в квадрате - единица измерения момента инерции в Международной системе единиц. Эта единица является производной в системе СИ. Килограмм - метр в квадрате - это момент инерции материальной точки, имеющей массу один килограмм, движущейся по окружность радиуса 1 метр, вокруг оси вращения.
Грамм - сантиметр в квадрате - единица измерения момента инерции в системе СГС
Если принять во внимание, что основными единицами измерения в системе СГС являются сантиметр, грамм и секунда, то используя определение момента инерции материальной точки (3), получим, что грамм - сантиметр в квадрате - единица измерения момента инерции в системе СГС:
\[\left[J\right]=г\cdot {см}^2.\]
Грамм, умноженный на сантиметр в квадрате - это момент инерции материальной точки, имеющей массу один грамм, находящейся на расстоянии один сантиметр от оси вращения.
Грамм-сантиметр в квадрате соотносится с единицей измерения момента инерции системы СИ как:
\[1\ г\cdot {см}^2=\ {10}^{-3}кг\cdot {\left({10}^{-2}\right)}^2={10}^{-7}кг\cdot м^2.\]
Момент инерции, не имеющий единицы измерения
Безразмерный момент инерции используют при изучении и описании движения и структуры небесных тел (планет, спутников и т. д). Безразмерным моментом инерции называют физическую величину, равную отношению момента инерции тела, обладающего радиусом $r$ и массой $m$, вращающегося около оси, к моменту инерции материальной точки равной массы ($m$), вращающейся относительно оси находящейся от точки на расстоянии $r$. Безразмерный момент инерции отображает распределение массы по глубине.
Тонкостенная сфера имеет безразмерный момент инерции равный $\frac{2}{3}$. Если масса тела сконцентрирована ближе к центру тела, то его безразмерный момент инерции меньше. У Луны имеющей структуру близкую к однородной, безразмерный момент инерции равен 0,391. Земля, обладающая плотным ядром, имеет безразмерный момент инерции 0,335.
Примеры задач с решением
Пример 1
Задание. Каким будет единица измерения момента инерции материальной точки, которая вращается около неподвижной оси, если получить ее из основного закона динамики вращательного движения?
Решение. Формулу закона динамики вращательного движения для материальной точки представим как:
\[\overline{M}=J\overline{\varepsilon \ }\left(1.1\right),\]
где $\overline{M}$ - суммарный момент сил, который действует на точку; $\overline{\varepsilon \ }$ - угловое ускорение с которым точка движется. Выразим момент инерции из (2.1):
\[J=\frac{\overline{M}}{\overline{\varepsilon }}\left(1.2\right),\]
тогда:
\[\left[J\right]=\frac{\left[M\right]\ }{\left[\varepsilon \right]}\left(1.3\right),\]
Единицей измерения момента сил в системе СИ является:
\[\left[M\right]=Н\cdot м=\frac{кг\cdot м}{с^2}м=\frac{кг\cdot м^2}{с^2}.\]
Угловое ускорение материальной точки найдем как:
\[\varepsilon =\frac{a_{\tau }}{R}\ \left(1.4\right),\]
где $a_{\tau }$ - тангенциальное ускорение точки; R - радиус окружности, по которой точка перемещается.
Значит:
\[\left[\varepsilon \right]=\frac{\left[a_{\tau }\right]}{\left[R\right]}=\frac{м}{с^2\cdot м}=\frac{1}{с^2}.\]
В соответствии с выражением (1.3) имеем:
\[\left[J\right]=\frac{кг\cdot м^2}{с^2}\cdot c^2=кг\cdot м^2.\]
Ответ. Исходя из основного закона динамики вращательного движения, получаем, что в системе СИ момент инерции измеряется в килограммах, умноженных на метр в квадрате.
Пример 2
Задание. Вычислите момент инерции Земного шара относительно его оси вращения. Считайте массу Земли и ее радиус известными. ($M_Z=5,97\cdot {10}^{24}кг;;\ R_Z=6371\ км$). Выразите момент инерции в $т\cdot м^2$ (тонна, умноженная на метр в квадрате)
Решение. Будем считать Землю однородным шаром. Найдем момент инерции шара, относительно оси, которая проходит через центр. Разобьем шара на диски (рис.1) толщина которых составляет $dh$, радиус ($r)\ $дисков изменяется, плоскости дисков которые перпендикулярны оси вращения.
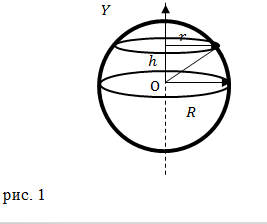
Из рис.1 очевидно, что:
\[r^2=R^2-h^2\ \left(2.1\right),\]
при этом -R$\le h\le $R.
Элементарный момент инерции (диска) запишем как:
\[dJ=\frac{dmr^2}{2}\ \left(2.2\right),\]
где масса выделенного диска ($dm=\rho dV$) равна:
\[dm=\rho \pi r^2dh\ \left(2.3\right).\]
Следовательно:
\[dJ=\frac{с$\eth${(R^2-h^2)}^2dh\ \ }{2}\ \left(2.4\right).\]
Получим момент инерции шара, относительно оси, которая проходит через его центр масс, интегрируя выражение (2.4) по объему шара:
\[J=\int\limits_V{dJ}=2\int\limits^R_0{\frac{\rho \pi {\left(R^2-h^2\right)}^2dh\ \ }{2}=\frac{8\pi \rho }{15}}R^5(2.5).\]
Плотность однородного шара равна:
\[\rho =\frac{m}{V}=\frac{3m}{4\pi R^3}\ \ \left(2.6\right),\]
то выражение (2.5) преобразуем к виду:
\[J=\frac{3m}{4$\eth$R^3}\frac{8$\eth$}{15}R^5=\frac{2}{5}{mR}^2(2.7).\]
Окончательно формулу для нахождения момента инерции Земного шара запишем как:
\[J=\frac{2}{5}{M_ZR_Z}^2.\]
Вычислим момент инерции Земли:
\[J=\frac{2}{5}{5,97•{10}^{24}\cdot (6,371\cdot {10}^6)}^2\approx 9,7\cdot {10}^{37}\left(кг\cdot м^2\right).\]
Для того, чтобы выразить момент инерции в $т\cdot м^2$, используем соотношение:
\[1\ т=1000\ кг,\ следовательно,\ 1\ т\cdot м^2=1000\ кг\cdot м^2.\]
Получаем:
\[J=9,7\cdot {10}^{37}кг\cdot м^2=9,7\cdot {10}^{34}т\cdot м^2.\]
Ответ. $J=9,7\cdot {10}^{34}т\cdot м^2$
Читать дальше: единицы измерения плотности.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 455 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!











