Единицы измерения длины, теория и онлайн калькуляторы
Единицы измерения длины
Процесс установки соответствия между свойством и числом, причем так, чтобы сравнение свойств можно было бы сделать с помощью сравнения чисел, носит название измерения. Одним из свойств тел является их протяженность. Протяженность тела в одном направлении, называют длиной тела. Рассмотрим две линейки. Для сравнения длины линеек приложим их друг другу так, чтобы один из концов первой линейки совпал с концом второй линейки. Вторые концы линеек либо совпадут, либо нет. При совпадении всех концов линеек они равны по длине. При измерении длине каждой линейки приписывается некоторое число, которое однозначно определяет ее протяженность. При этом число позволяет выбрать из всех линеек однозначно такие, длина которых определяется этим числом. Так определяемое свойство, называют физической величиной. При этом процесс нахождения числа, характеризующего физическое свойство, называют измерением.
Для единиц длины установлены соответствующие эталоны, при сравнении с которыми определяют любую длину.
Метр - единица измерения длины (расстояния) в метрических системах
Длина и расстояние в Международной системе единиц (СИ) измеряется в метрах (м). Метр является основной единицей системы СИ. Кроме системы СИ метр служит основной единицей и при помощи него измеряют расстояние в некоторых других системах. Например, метр единица измерения длины в МКС (система в которой основными считали три единицы: метр, килограмм, секунду). В настоящее время МКС не считается самостоятельной системой. Системы в которых метр - единица измерения длины (расстояния), а килограмм - единица измерения массы, называют метрическими.
По определению 1 метр - это длина пути, который проходит свет в вакууме за $\frac{1}{299792458}$ секунды.
При измерениях и вычислениях используют кратные и дольные единицы метра как единицы измерения длины (расстояния). Например, ${10}^{-10}$м = 1А (ангстрем); ${10}^{-9}$м = 1 нм (нано метр); 1 км =1000 м.
В настоящее время в нашей стране чаще всего используют Международную систему единиц измерения (СИ).
Единицы измерения длины в не метрических системах
Существуют системы единиц, в которых сантиметры - единицы измерения длины, например система СГС. Система СГС много применялась до того, как была принята Международная система единиц. Иначе ее называют абсолютной физической системой единиц. В ее рамках основными считают 3 единицы измерения: сантиметр, грамм, секунду.
Существуют национальные системы единиц измерения длины и расстояния. Так, например, Британская система не является метрической. Единицами измерения длины и расстояния в этой системе служат: миля, фурлонг, чейн, род, ярд, фут и другие непривычные нам единицы. $1\ миля=1,609\ км;;$ 1 фурлонг =201,6 м; 1 чейн-20,1168 м. Японская система измерения длины и расстояния, также отличается от метрической. В ней используют, например, такие единицы измерения длины как: мо, рин, бу, сяку и другие. 1 мо=0,003030303 см; 1 рин =0,03030303 см; 1 бу=0,30303 см.
Используются профессиональные системы измерения длины и расстояния. Например, существует типографическая система, морская (используемая на флоте), в астрономии используют специальные виды единиц измерения расстояний. Так, в астрономии расстояние от Земли до Солнца является астрономической единицей (а.е) измерения длины (расстояния).
1 а.е=149~597 870,7 км, что равно расстоянию от Солнца до Земли. Световой год равен 63241,077 а.е. Парсек $\approx 206264,806247\ а.е$.
Некоторые единицы измерения длины, ранее применявшиеся в нашей стране, сейчас не используются. Так, в старорусской системе существовали: пядь, стопа, локоть, аршин, мера, верста и другие единицы. 1 пядь = 17,78 см; 1 стопа = 35,56 см; 1 мера = 106,68 см; 1 верста = 1066,8 метра.
Примеры задач с решением
Пример 1
Задание. Какова длина электромагнитной волны ($\lambda $), если энергия фотона составляет $\varepsilon ={10}^{-18}Дж$? Каковы единицы измерения длины электромагнитной волны?
Решение. В качестве основы для решения задачи используем формулу для определения энергии фотона в виде:
\[\varepsilon =h\nu \ \left(1.1\right),\]
где $h=6,62\cdot {10}^{-34}$Дж$\cdot c$; $\nu $ - частота колебаний в электромагнитной волне, она связана с длиной волны света как:
\[\nu =\frac{c}{\lambda }\ \left(1.2\right),\]
где $c=3\cdot {10}^8\frac{м}{с}$ - скорость света в вакууме. Учитывая формулу (1.2) выразим из (1.1) длину волны:
\[\varepsilon =h\nu =\frac{hc}{\lambda }\to \lambda =\frac{hc}{\varepsilon }\left(1.3\right).\]
Проведем вычисления длины волны:
\[\lambda =\frac{6,62\cdot {10}^{-34}\cdot 3\cdot {10}^8}{{10}^{-18}}=1,99\cdot {10}^{-7\ }\left(м\right).\]
Ответ. $\lambda =1,99\cdot {10}^{-7\ }$м=199 нм. Метры - единицы измерения длины электромагнитной волны
(как и любой другой длины) в системе СИ.
Пример 2
Задание. Тело упало с высоты, равной $h=1\ $км. Какова длина пути ($S$), которое пройдет тело за первую секунду падения, если начальная скорость его равна нулю? \textit{}
Решение. По условию задачи имеем:
\[v_0=0\frac{м}{с};;t=1\ c.\]
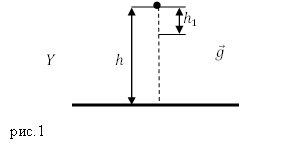
В данной задаче мы имеем дело с равноускоренным движением тела в поле тяжести Земли. Это означает, что тело движется с ускорением $\overline{g}$, которое направлено по оси Y (рис.1). За основу решения задачи примем уравнение:
\[\overline{s}={\overline{s}}_0+{\overline{v}}_0t+\frac{\overline{g}t^2}{2}\ \left(2.1\right).\]
Начало отсчета поместим в точку начала движения тела, учтем, что начальная скорость тела равно нулю, тогда в проекции на ось Y выражение (2.1) запишем как:
\[s=h_1=\frac{gt^2}{2}.\]
Проведем вычисления длины пути тела:
\[h_1=\frac{9,8\cdot 1^2}{2}=4,9\ (м).\]
Ответ. $h_1=4,9\ $м, расстояние, которое пройдет тело в первую секунду своего движения не зависит от высоты, с которой оно упало.
Читать дальше: единицы измерения массы.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 468 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!











