Давлением в физике называют физическую величину, которая равна пределу отношения нормальной силы ($\Delta F_n$), действующей на единицу поверхности тела:

\[p={\mathop{\lim }_{\Delta S\to 0} \frac{\Delta F_n}{\Delta S}\ }=\frac{dF_n}{dS}\left(1\right),\]

$\Delta S$ - площадь участка тела, на которое действует сила $\overline{F}$.

Задание. Поршень на рис.1 смещают влево на $\Delta l=$4 см. Площадь поршня равна $S=$48 ${см}^2$. Объем воздуха в резервуаре первоначально составлял $V_1=480\ {см}^3$, давление при этом было равно одой атмосфере ($p_1=1\ атм.$). Какую силу следует приложить к поршню для того чтобы удержать его при смещении?

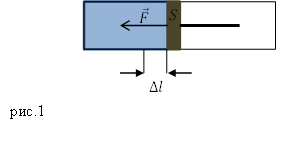
Решение. В результате перемещения поршня влево появляется избыточное давление на поршень со стороны газа внутри сосуда. Это давление можно компенсировать, если приложит к поршню силу, равную:

\[F=\Delta pS=S\left(p_2-p_1\right)\left(1.1\right),\]

где $p_2$ - давление, которое под поршнем после того как его сдвинули в левую сторону.

Будем считать, что процесс, который проводят в нашей системе, является изотермическим, а газ под поршнем идеальным. Тогда поведение газа подчиняется закону Бойля - Мариотта:

\[p_1V_1=p_2V_2\left(1.2\right),\]

где $V_2$ - давление, которое занимает газ после того, как поршень передвинули. Его можно найти как:

\[V_2=V_1-\Delta lS\ \left(1.3\right).\]

Выразим давление $p_2$ из (1.2), примем во внимание формулу (1.3), имеем:

\[p_2=\frac{p_1V_1}{V_2}=\frac{p_1V_1}{V_1-\Delta lS}\ \left(1.4\right).\]

Подставим правую часть выражения (1.4) в (1.1), получим:

\[F=S\left(\frac{p_1V_1}{V_1-\Delta lS}-p_1\right)=S^2p_1\frac{\Delta l}{V_1-S\Delta l}\ (1.5).\]

Прежде чем проводить вычисления разберемся с единицами измерения величин. По условию $p_1$= 1 атм. в системе СИ паскаль - единица измерения давления, следовательно, считаем, что $p_1$= 1 атм$\approx {10}^5Па$. Переведем $S$=48 ${см}^2=48\cdot {10}^{-4}м^2$; $\Delta l=0,04\ м;;\ V_1$=$4,80\cdot {10}^{-4}м^3$ Поведем вычисления:

\[F={\left(48\cdot {10}^{-4}\right)}^2\cdot {10}^5\frac{0,04}{4,80\cdot {10}^{-4}-0,04\cdot 48\cdot {10}^{-4}}=32\left(Н\right).\]

Проверим размерности правой и левой части выражения (1.5), имеем:

\[\left[F\right]=H={\left(м^2\right)}^2\frac{Н}{м^2}\frac{м}{м^3-м^2м}=Н.\]

Ответ. F=32 Н

Задание. Проверьте, какая единица измерения получается у давления в уравнении состояния идеального газа Клапейрона Менделеева.

Решение. Уравнение состояния идеального газа (уравнение Менделеева - Клапейрона) имеет вид:

\[pV=\nu RT\ \left(2.1\right).\]

Из этого уравнения давление получается равным:

\[p=\frac{\nu RT}{V}\ \left(2.1\right).\]

Разберемся с единицами измерения величин, которые стоят в правой части формулы (2.1):

$\left[\nu \right]=моль;;\ \left[T\right]=K;;\ R=8,31\ \frac{Дж}{моль\cdot К};;\ \left[V\right]=м^3;;$ Учтем, что:

$1\ Дж=\ 1Н\cdot м\ \left(2.2\right).$Тогда получаем:

\[\left[p\right]=Па=\frac{моль}{м^3}\cdot \frac{Дж}{моль\cdot К}\cdot К=\frac{Н\cdot м}{м^3}=\frac{Н}{м^2}=Па\]

Ответ. Получили паскаль.