Спираль Корню в физике, теория и онлайн калькуляторы
Спираль Корню
В одномерных задачах разбивать волновой фронт на кольцевые зоны не всегда рационально. Так, рассматривая дифракцию на прямоугольной щели, например, волновой фронт разбивают на полосатые зоны, которые называют зонами Шустера. Допустим, что волновой фронт плоский. Плоскость этого фронта (AB) перпендикулярна плоскости рис.1.
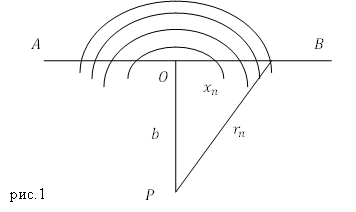
Величина $b$- это длина перпендикуляра, который опущен из точки наблюдения ($P$) на волновой фронт. Выделим цилиндрические коаксиальные поверхности с осью в точке $P$, перпендикулярной плоскости рисунка. Радиусы этих поверхностей будут: $b,\ b+\frac{\lambda }{2}$, $b+2\frac{\lambda }{2}$, ..., где $\lambda $ - длина волны. При этом волновой фронт будет разбит на прямоугольные полосы. называемые зонами Шустера. Центральную зону, обычно считают как две зоны, одна зона расположена правее точки О, другая левее. В таком случае ширины последовательных зон Шустера равны:
\[\sqrt{b\lambda },\ \left(\sqrt{2}-1\right)\sqrt{b\lambda },\ \left(\sqrt{3}-\sqrt{2}\right)\sqrt{b\lambda },\ \dots \left(1\right).\]
Из последовательности (1) видно, что ширина зон Шустера убывает и при $r\to \infty $ она равна$\ \frac{{\rm \ }\lambda }{2}$. Обычно имеют значение несколько десятков первых зон Шустера.
Графический метод. Спираль Корню
Проведем разбиение каждой зоны Шустера на узкие полоски. Колебания в точке наблюдения ($P$), которое вносит каждая полоска, будем изображать вектором на векторной диаграмме. Перейдем к пределу, уменьшая ширину каждой полоски почти до нуля. В результате такого построения получают плавную кривую, которая называется спиралью Корню (рис.2).
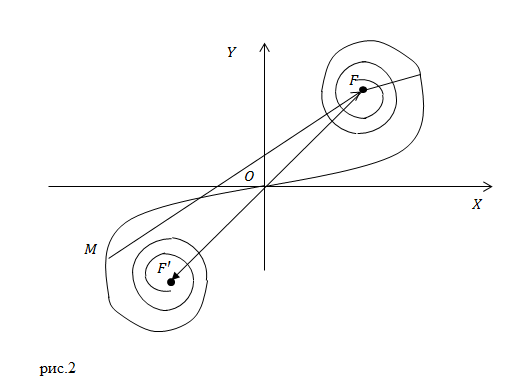
Кривая Корню состоит из двух симметричных ветвей, которые бесконечное количество раз, обвиваются вокруг фокусов $F\ $ и $F'$, при этом бесконечно близко приближаются к этим фокусам. Верхняя ветвь отражает действие правой половины волнового фронта, нижняя половина - левой половины.
Начальные зоны Шустера убывают быстрее, чем зоны Френеля.
Колебание, которое возбуждается первой правой зоной Шустера, изображают вектором $\overline{OA}$, второй правой зоной вектором $\overline{A2}$, двумя первыми правыми зонами - вектором $\overline{O2}$ и т.д. Весь фронт волны возбуждает колебание, которое представляет вектор $\overline{F'F}$, соединяющий фокусы спирали. При приближении фокусам амплитуда колебаний уменьшается, она в пределе переходит в ноль.
Уравнение спирали Корню
Поле волны в точке $P$ представлено интегралом:
\[E_P=\iint{e^{-ik\ \left(x^2+y^2\right)/(2b)}dxdy\ \left(2\right).}\]
Интегрирование выполняют по всей открытой поверхности фронта волны. Пусть в направлении оси Y волна распространяется далеко в обе стороны. Тогда при интегрировании считаем, что $-\infty \le y\le \infty $, в результате интегрирования по y получим постоянный множитель, не представляющий интереса. Интегрирование по $x$ проводят от нуля, считают верхний пердел изменяющимся. Обычно вместо $x$ вводят переменную $s$, равную:
\[s=\sqrt{\frac{kx^2}{b\pi }}\left(3\right).\]
При такой замене интеграл (2) преобразуется к виду:
\[E_P=\int\limits^s_0{e^{\frac{-i\pi s^2}{2}}ds\left(4\right)\ и\ }{E^*}_P=\int\limits^s_0{e^{\frac{i\pi s^2}{2}}ds\left(5\right).\ \ }\]
Изображая колебания используют выражения и (4) и (5). Строя спираль Корню чаще используют комплексно сопряженное выражение (5). Уравнение (5) является аналитической записью для спирали Корню в комплексной форме.
В координатной форме уравнение спирали Корню записывают как:
\[\left\{ \begin{array}{c}
X\left(s\right)=\int\limits^s_0{{\cos \left(\frac{\pi s^2}{2}\right)ds,\ }} \\
Y\left(s\right)=\int\limits^s_0{{\sin \left(\frac{\pi s^2}{2}\right)ds\ }} \end{array}
\left(6\right).\right.\]
Интегралы системы (6) называют интегралами Френеля. Из выражений (6) видно, что:
\[X\left(s\right)=-X\left(-s\right);;Y\left(s\right)=-Y\left(-s\right)\left(7\right).\]
Формулы (7) показывают, что кривая Корню симметрична относительно начала координат.
Координаты фокусов спирали находят, полагая $s=\infty $, при этом:
\[X_F=Y_F=\frac{1}{2},\ X_{F'}=Y_{F'}=-\frac{1}{2}\left(8\right).\]
Дифференциал дуги спирали Корню находят из равенства:
\[\left|ds\right|=\left|e^{\frac{i\pi s^2}{2}}\right|\left(9\right).\]
Параметр $s$ - длина дуги спирали, берущая свое начало от точки О.
Принимая $\tau $ за угол между касательной к спирали Корню и осью X имеем:
\[tg\ \tau =\frac{dY}{dX}=tg\ \left(\frac{\pi s^2}{2}\right)\left(10\right).\]
Формула (10) дает возможность наглядно проследить, как кривая обвивается около фокусов. При $s=0,\ \tau =0$, что означает, что спираль Корню касается оси X в начале координат. При $s=1$ кривая идет вверх, $s=\sqrt{2\ }\to \tau =\pi $, касательная к спирали снова горизонтальна, но идет в отрицательном направлении.
Формула кривизны спирали ($R$) имеет вид:
\[\frac{1}{R}=\frac{d\tau }{ds}=\pi s\ \left(11\right).\]
Длина всей спирали бесконечна, при приближении к фокусам кривизна стремится к бесконечности.
Работая со спиралью Корню необходимо знать величину параметра $s$. Его находят, зная расстояние $x$ точки наблюдения от центра картины O (рис.1). Вычислив ширину первой зоны Шустера $\sqrt{b\lambda },$ находят:
\[s=x\sqrt{\frac{2}{\lambda b}}\left(12\right).\]
Спираль Корню является инструментом анализа дифракции. Она позволяет понять каково количественное распределение интенсивности в дифракционной картине.
Примеры задач с решением
Пример 1
Задание. Рассмотрите механизм нахождения распределения интенсивности, применяя спираль Корню. Для края геометрической тени в случае дифракции плоской волны от прямого края непрозрачной полуплоскости (рис.3).
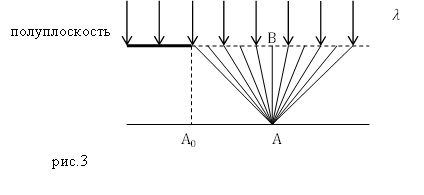
Решение. Если точка $А$ расположена правее $А_0$ (рис.3), то правая часть волновой поверхности является полностью открытой (от точки B). Тогда на спирали амплитуда колебаний в точке наблюдения соответствует вектору $\overline{MF}$ (рис.2). Начало вектора $\overline{MF}$ определяет положение точки наблюдения. Если точкой наблюдения является точка $A_0\ $(край геометрической тени), то точка начала вектора $\overline{MF}\ $совпадет с точкой О
спирали Корню, Амплитуда колебаний изображается при помощи вектора $\overline{OF}$:
\[\overline{OF}=\frac{1}{2}\overline{F'F}\left(1.1\right).\]
Интенсивность света в точке $A_0$ в четверо меньше интенсивности, если бы фронт волны был полностью открыт.
Допустим, что точка наблюдений перемещается в правую сторону от точки $A_0$, тогда начало вектора на спирали Корню переместится по левой ветке спирали (слева от точки B открываются новые зоны). В результате амплитуда и интенсивность в точке A изменяется от максимальной к минимальной. При этом интенсивность света приближается к интенсивности падающего света.
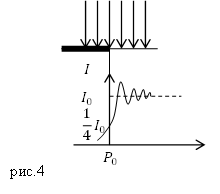
Если точка наблюдения движется от точки $A_0$ в область геометрической тени, то начало вектора на спирали Корню переместится правее точки О. В таком случае длина вектора, следовательно, интенсивность света монотонно уменьшается до нуля (рис.4).
Пример 2
Задание. Как проходит касательная к спирали Корню, при $s=\sqrt{3}$; $s=2.$
Решение. За основу решения задачи примем выражение для угла касательной к спирали Корню:
\[tg\ \tau =tg\ \left(\frac{\pi s^2}{2}\right)\to \tau =\frac{\pi s^2}{2}\left(2.1\right).\]
Получаем при $s=\sqrt{3}$:
\[\tau =\frac{\pi {(\sqrt{3})}^2}{2}=\frac{3}{2}\pi (2.2).\]
При $s=\sqrt{3}$ касательная идет вертикально вниз.
При $s=2$ имеем:
\[\tau =\frac{\pi {(2)}^2}{2}=2\pi (2.3).\]
Из выражения (2.3) следует, что касательная горизонтальна (исходное положение).
Ответ. 1) При $s=\sqrt{3}$ касательная идет вертикально вниз. 2) При $s=2$ касательная горизонтальна.
Читать дальше: теорема о циркуляции вектора напряженности.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 472 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!














