Свободными называют заряды, которые могут под воздействием электрического поля перемещаться за значительные расстояния.
Свободные и связанные заряды
Определение свободных и связанных зарядов
Свободными являются электроны в проводниках, ионы в газах, заряды на поверхности диэлектрика, которые попали на него снаружи, нарушающие нейтральность этих веществ.
Заряды, которые входят в состав нейтральных молекул диэлектриков, ионы, закрепленные в узлах кристаллических решеток у положений своего равновесия, являются связанными зарядами.
Проводники и свободные заряды в них
Проводником называют вещества, в которых свободные заряды могут двигаться по всему объему.
Проводниками являются металлы, щелочи, кислоты, солевые растворы и т.д.
При помещении проводника во внешнее электрическое поле происходит разделение зарядов противоположного знака. Данное явление называют электростатической индукцией. Как только проводник попал в электрическое поле, свободные заряды начинают двигаться. Перераспределение этих зарядов изменяет электрическое поле. Движение зарядов происходит до тех пор пока напряженность электрического поля внутри проводника не станет равна нулю. Отметим, что свободные заряды распределены на поверхности проводника таким образом, что $\overline{E}\ $ перпендикулярен проводящей поверхности в каждой ее точке. Поверхность проводника - это эквипотенциальная поверхность не зависимо от ее формы.
В равновесии заряды распределены так, что равнодействующая всех сил, приложенных к каждому заряду, была равна нулю. Следовательно, необходимым условием электростатического равновесия является равенство нулю напряженности электростатического поля внутри проводника ($\overline{E}=0$). Если бы внутри проводника имелось электрическое поле, то свободные заряды двигались, что говорит об отсутствии равновесия. Условие $\overline{E}=0$ выполняется для всех точек внутри проводника и это не зависит от того, заряжен он сам или находится во внешнем электростатическом поле.
Условие отсутствие электростатического поля внутри проводника ведет к тому, что заряды распределяются только на поверхности проводника.
Используя теорему Гаусса можно получить формулу, определяющую напряженность электростатического поля около поверхности проводника. Выделим на поверхности проводника элемент $\Delta S$, который можно считать плоским, поверхностную плотность заряда на нем постоянной ($\sigma $). Построим замкнутую цилиндрическую поверхность составляющие которой перпендикулярны поверхности проводника, а основания параллельны $\Delta S$ (рис.1). При этом нижнее основание нашего цилиндра находится внутри проводника, где $\overline{E}=0,$ а верхнее у поверхности проводника, где силовые линии перпендикулярны поверхности.
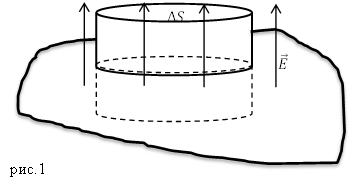
При таком выборе поверхности поток напряженности проходит только через верхнее основание выделенного цилиндра, тогда по теореме Гаусса - Остроградского имеем:
\[Ф_E=E\Delta S=\frac{q}{{\varepsilon }_0}\to E\Delta S=\frac{\sigma \Delta S}{{\varepsilon }_0}\to E=\frac{\sigma }{{\varepsilon }_0}\left(1\right).\]Формула (1) дает напряжённость полного электростатического поля, которое существует около поверхности проводника, независимо от того, создается ли это поле только самим проводником, несущим заряд или еще другими зарядами.
Диэлектрики и связанные заряды в них
Диэлектриками называют вещества, которые в обычном состоянии содержат только связанные заряды. Примерами диэлектриков являются: дистиллированная вода, масла, стекло, фарфор и т.д.
Если диэлектрик поместить в электрическое поле, то заряды не могут разделиться, так как свободных зарядов нет. В таком случае происходит поляризация, то есть процесс смещения зарядов, имеющих противоположные знаки в пределах молекулы (или атома). В результате поляризации на поверхности диэлектрика возникают связанные заряды. При этом, вектор напряженности поля, создаваемого связанными зарядами, имеет направление противоположное вектору напряженности внешнего поля. При этом говорят, что диэлектрик ослабляет электрическое поле в $\varepsilon $раз по сравнению с тем же полем в вакууме. $\varepsilon $- диэлектрическая проницаемость вещества.
Примеры задач с решением
Задание. Как, используя теорему Гаусса - Остроградского, показать, если проводник заряжен, избыточный заряд распределяется по его поверхности?
Решение. Рассмотрим произвольную замкнутую поверхность, которая выделяет некоторый объем внутри проводника ($V$) (рис.2).
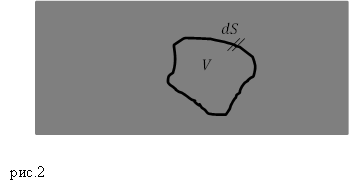
Во всех точках этой поверхности напряженность электрического поля равна нулю:
\[\overline{E}=0\ \left(1.1\right).\]Это означает, что поток напряженности через данную поверхность равен нулю:
\[Ф_S=\int\limits_S{\overline{E}d\overline{S}}=\overline{E}\int\limits_S{d\overline{S}=}0\left(1.2\right).\]По теореме Гаусса:
\[Ф_S=\frac{q}{{\varepsilon }_0}\ \left(1.3\right).\]Из выражений (1.2) и (1.3) следует, что полный заряд в выделенном объеме, ограниченном рассматриваемой поверхностью равен нулю:
\[q=0.\]Так как мы выбирали поверхность произвольно, то результат можно применить к любому участку внутри проводника до его поверхности.
Ответ. Мы получили, что у проводника избыточный заряд распределен по его поверхности.
Задание. От чего зависит плотность распределения заряда на поверхности проводника?
Решение. Если заряженный проводник является уединенным, то плотность заряда ($\sigma $) тем больше, чем больше полный заряд проводника ($q$). Допустим, что проводник является шаром. В таком случае заряд распределен по поверхности равномерно так, что:
\[\sigma =\frac{q}{S}=\frac{q}{4\pi R^2}\left(2.1\right).\]Напряженность поля, которое создает заряженный шар, около его поверхности равна:
\[E=\frac{q}{{4\pi \varepsilon }_0R^2}\left(2.2\right).\]Принимая во внимание (2.1), имеем:
\[E=\frac{\sigma 4\pi R^2}{{4\pi \varepsilon }_0R^2}=\frac{\sigma }{{\varepsilon }_0}\left(2.3\right).\]Выражение (2.3) выполняется в общем случае, а не только для заряженного шара. Величину $\sigma $ можно выразить через потенциал шара, зная, что:
\[\varphi =\frac{q}{4\pi {\varepsilon }_0R}\to q=4\pi {\varepsilon }_0R\varphi \left(2.4\right).\]Учитывая (2.4) и (2.1), получаем:
\[\sigma =\frac{4\pi {\varepsilon }_0R\varphi }{4\pi R^2}=\frac{{\varepsilon }_0}{R}\varphi \left(2.5\right).\]Какой сложной не была бы форма проводника, потенциал проводящего тела во всех точках одинаков. Значит, поверхностная плотность заряда будет больше там, где меньше R, то есть, где кривизна поверхности больше. В этих же местах будет больше напряженность электрического поля.
Читать дальше: система СИ (единицы измерения).










