Классический закон сложения скорости и ускорения материальной точки
Классический закон сложения скорости и ускорения материальной точки
Сложное движение материальной точки
Допустим, что материальная точка движется относительно системы координат XYZ, а сама система координат XYZ перемещается относительно системы координат $X_1Y_1Z_1$, которая неподвижна (рис.1).
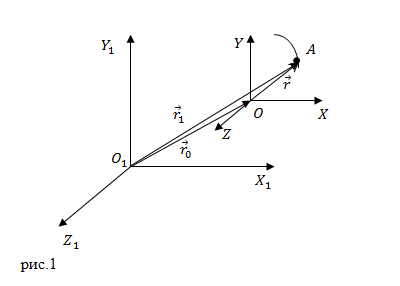
Движение точки А, рассматриваемое одновременно относительно двух систем координат, подвижной и неподвижной называют сложным движением.
При этом перемещение точки относительно неподвижной системы координат называют абсолютным движением. Скорость и ускорение движения точки относительно неподвижных осей называют абсолютной скоростью ($\overline{v}$) и абсолютным ускорением ($\overline{a}$).
Перемещение материальной точки по отношению к движущейся системе координат называют относительным. Скорость и ускорение точки относительно подвижной системы координат называют относительными. Обозначим их ${\overline{v}}_r$ и ${\overline{a}}_r$.
Перемещение подвижной системы координат вместе со связанными с ней геометрическими точками относительно неподвижной системы называют переносным движением. При этом переносной скоростью (${\overline{v}}_e$) и переносным ускорением (${\overline{a}}_e$) точки $A$ называют скорость и ускорение по отношению к неподвижной системе координат точки $A_1$, которая связана с подвижными осями, с которой в данный момент времени совпадает перемещающаяся точка $A$. Точка $A$ в процессе своего движения оказывается в разных местах системы координат XYZ. Точка $A_1$ движется вместе с системой координат XYZ относительно неподвижной системы $X_1Y_1Z_1$, со скоростью ${\overline{v}}_{A_1}\ и\ $ускорением${\ \overline{a}}_{A_1}$. Эти величины и есть переносные скорость и ускорение:
\[{\overline{v}}_e={\overline{v}}_{A_1};;\ {\overline{a}}_e={\ \overline{a}}_{A_1}=\frac{d{\overline{v}}_{A_1}}{dt}\left(1\right).\]
В практических задачах роль систем координат выполняют подвижные и неподвижные тела. Переносное движение сводится к одному из видов движения: поступательному, вращательному и т.д.
Скорости и ускорения связаны теоремами сложения скоростей и ускорений.
Теорема сложения скоростей
Обозначим ${\overline{r}}_1$ - радиус-вектор точки A, который проведен из начала неподвижной системы координат; $\overline{r}$ - радиус - вектор, который проведен из начала подвижной системы координат к точке A; ${\overline{r}}_0$ - радиус-вектор подвижного начала относительно неподвижного (рис.1).
Абсолютная скорость точки A равна:
\[\overline{v}=\frac{d{\overline{r}}_1}{dt}\left(2\right).\]
Относительная скорость может быть выражена как:
\[{\overline{v}}_r=\frac{\tilde{d}\overline{r}}{dt}=\frac{d}{dt}\left[(x\overline{i}+y\overline{j}+z\overline{k})\right]=\frac{dx}{dt}\overline{i}+\frac{dy}{dt}\overline{j}+\frac{dz}{dt}\overline{k}\left(3\right),\]
где $\tilde{d}$ - знак тильда обозначает производную в подвижной системе координат. $\overline{i}=const;;\overline{j}=const;;\ \overline{k}=const.\ \ $Производную относительно подвижной системы координат называют относительной или локальной, вычисляя эту производную движение осей считают остановленным.
Переносная скорость точки A есть производная от радиус-вектора точки $A'$ подвижной системы координат, вычисленной относительно неподвижной системы координат:
\[{\overline{v}}_e={\overline{v}}_{A_1}=\frac{d{\overline{r}}_{A_1}}{dt}=\frac{d}{dt}\left({\overline{r}}_0+\overline{OA_1}\right)=\frac{d}{dt}\left({\overline{r}}_0+(x\overline{i}+y\overline{j}+z\overline{k})\right)=\frac{d{\overline{r}}_0}{dt}+x\frac{d\overline{i}}{dt}+y\frac{d\overline{j}}{dt}+z\frac{d\overline{k}}{dt}\left(4\right),\]
где $x=const;;\ y=const;;z=const.$
Из рис.1 видно, что:
\[{\overline{r}}_1={\overline{r}}_0+\overline{r}\left(5\right).\]
Найдем производную по времени от (5), имеем:
\[\frac{d{\overline{r}}_1}{dt}=\frac{d{\overline{r}}_0}{dt}+x\frac{d\overline{i}}{dt}+y\frac{d\overline{j}}{dt}+z\frac{d\overline{k}}{dt}+\frac{dx}{dt}\overline{i}+\frac{dy}{dt}\overline{j}+\frac{dz}{dt}\overline{k}\left(6\right).\]
Применяя принятые нами обозначения:
\[\overline{v}={\overline{v}}_e+{\overline{v}}_r\left(7\right).\]
Формула (7) - закон сложения скоростей. С точки зрения геометрии мы получили, что абсолютная скорость при сложном движении точки отображается направленной диагональю параллелограмма, сторонами которого являются векторы относительной и переносной скорости.
Теорема сложения ускорений
Относительное ускорение определяет быстроту изменения относительной скорости в отношении подвижной системы координат. Значит, его можно выразить при помощи локальной производной по времени от ${\overline{v}}_r$ точки:
\[{\overline{a}}_r=\frac{d\ {\overline{v}}_r}{dt}=\frac{d^2x}{dt^2}\overline{i}+\frac{d^2y}{dt^2}\overline{j}+\ \frac{d^2z}{dt^2}\overline{k}\left(8\right),\]
где $\overline{i}$, $\overline{j}$, $\overline{k}$ - постоянные единичные орты.
Переносное ускорение в соответствии с (8) равно:
\[{\overline{a}}_e={\ \overline{a}}_{A_1}=\frac{d}{dt}\left[\frac{d{\overline{r}}_O}{dt}+x\frac{d\overline{i}}{dt}+y\frac{d\overline{j}}{dt}+z\frac{d\overline{k}}{dt}\right]=\frac{d^2{\overline{r}}_O}{dt^2}+x\frac{d^2\overline{i}}{dt^2}+y\frac{d^2\overline{j}}{dt^2}+z\frac{d^2\overline{k}}{dt^2}\left(9\right),\]
где $x=const,\ y=const,\ z=const.$
Абсолютное ускорение точки определяет скорость изменения соответствующей скорости относительно неподвижных осей:
\[\overline{a}=\frac{d\overline{v}}{dt}=\frac{d}{dt}\left({\overline{v}}_e+{\overline{v}}_r\right)=\frac{d{\overline{v}}_e}{dt}+\frac{d{\overline{v}}_r}{dt}\left(10\right).\]
Производные находят относительно неподвижных осей, переменными будут и координаты и орты.
\[\overline{a}={\overline{a}}_e+{\overline{a}}_r+2\left(\frac{dx}{dt}\cdot \frac{d\overline{i}}{dt}+\frac{dy}{dt}\cdot \frac{d\overline{j}}{dt}+\frac{dz}{dt}\cdot \frac{d\overline{k}}{dt}\right)\left(11\right).\]
Слагаемое $2\left(\frac{dx}{dt}\cdot \frac{d\overline{i}}{dt}+\frac{dy}{dt}\cdot \frac{d\overline{j}}{dt}+\frac{dz}{dt}\cdot \frac{d\overline{k}}{dt}\right)$ называют ускорением Кориолиса (${\overline{a}}_k$):
\[{\overline{a}}_k=2\left(\frac{dx}{dt}\cdot \frac{d\overline{i}}{dt}+\frac{dy}{dt}\cdot \frac{d\overline{j}}{dt}+\frac{dz}{dt}\cdot \frac{d\overline{k}}{dt}\right)=2\left[{\overline{\omega }}_e{\overline{v}}_r\right]\left(12\right),\]
где ${\overline{\omega }}_e$ - вектор переносной угловой скорости; ${\overline{v}}_r$ - вектор относительной линейной скорости; в правой части формулы (12) стоит векторное произведение.
И так, теорему сложения ускорений записывают в виде системы векторных уравнений:
\[\left\{ \begin{array}{c}
\overline{a}={\overline{a}}_e+{\overline{a}}_r+{\overline{a}}_k \\
{\overline{a}}_k=2\left[{\overline{\omega }}_e{\overline{v}}_r\right] \end{array}
\right.\left(13\right).\]
Для того чтобы определить величину и направление ускорения Кориолиса находят величину и направление ${\overline{v}}_r$. Далее строят вектор ${\overline{\omega }}_e$ и переносится в точку $A$. После этого используют правила векторной алгебры для вычисления векторного произведения. Ускорение Кориолиса направлено перпендикулярно плоскости, в которой находятся ${\overline{v}}_r$ и ${\overline{\omega }}_e$ в сторону, из которой кратчайший поворот от ${\overline{\omega }}_e$ к ${\overline{v}}_r,$ виден происходящим против часовой стрелки.
Примеры задач с решением
Пример 1
Задание. Человек сидит в вагоне поезда, который движется со скоростью ${\overline{v}}_e$ по горизонтальной дороге. Он видит через окно, что траектории капель дождя наклонены относительно вертикали под углом $\alpha .$ Какова абсолютная скорость падения капель, если дождь идет отвесный? Трение капель о стекло не учитывать.
Решение. Движение капель дождя будем рассматривать как сложное. Из теоремы сложения скоростей мы знаем, что:
\[\overline{v}={\overline{v}}_e+{\overline{v}}_r\left(1.1\right),\]
где ${\overline{v}}_r$ - скорость капли относительно стекла вагона; ${\overline{v}}_e$ - переносная скорость (скорость вагона относительно Земли).
Построим диаграмму скоростей (рис.2).
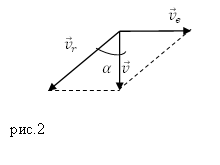
Из рис.2 видно, что:
\[v=\frac{v_e}{tg\ \alpha }.\]
Ответ. $v=\frac{v_e}{tg\ \alpha }$
Пример 2
Задание. Запишите теорему сложения ускорений для поступательного движения материальной точки.
Решение. Ускорение Кориолиса определяется как:
\[{\overline{a}}_k=2\left[{\overline{\omega }}_e{\overline{v}}_r\right]\left(2.1\right).\]
Модуль $\left|{\overline{a}}_k\right|$ равен:
\[\left|{\overline{a}}_k\right|=2\left|{\overline{\omega }}_e\right|\left|{\overline{v}}_r\right|{\sin \alpha \ \left(2.2\right),\ }\]
где $\alpha $ - угол между векторами ${\overline{\omega }}_e$ и ${\overline{v}}_r$.
Из выражения (2.2) следует, что ${\overline{a}}_k$=0, когда переносное движение является поступательным. В этом случае движение подвижной системы отсчета не имеет вращательной компоненты, переносная угловая скорость в любой момент времени равна нулю:
\[{\overline{\omega }}_e\equiv 0\left(2.3\right),\]
тогда в любой момент времени равно нулю ускорение Кориолиса. Теорема сложения ускорений принимает вид:
\[\overline{a}={\overline{a}}_e+{\overline{a}}_r\left(2.4\right).\]
Ответ. $\overline{a}={\overline{a}}_e+{\overline{a}}_r$
Читать дальше: магнитная восприимчивость и магнитная проницаемость.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 456 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!












