Векторная величина, обозначаемая $\overline{D}$, равная:
\[\overline{D}={\varepsilon }_0\overline{E}+\overline{P}\left(3\right),\]где $\overline{P}$ - вектор поляризации.
Вектор электрической индукции
Допустим, что одно вещество имеет диэлектрическую проницаемость равную ${\varepsilon }_1$, а вторая ${\varepsilon }_2$, тогда нормальная составляющая вектора напряженности электростатического поля ($E_n$) уменьшается во столько раз, во сколько увеличивается диэлектрическая проницаемость среды:
\[{\varepsilon }_1E_{n1}={\varepsilon }_2E_{n2}\left(1\right),\]где $E_{n1}$ - нормальная компонента напряженности поля в веществе 1; $E_{n2}$ - нормальная составляющая электростатического поля во втором веществе. Отметим, что при переходе из одного вещества в другое тангенциальная компонента вектора напряженности ($E_{\tau }$) изменяется без скачка. Говорят, что на границе двух веществ происходит «преломление» силовых линий поля.
Для сохранения всех преимуществ, которые дает теорема Остроградского - Гаусса при рассмотрении электростатического поля в вакууме, в веществе вводят физическую величину, которая не испытывает скачка при переходе из одного вещества в другое с разными $\varepsilon $.
Так как при переходе из вакуума в вещество с диэлектрической проницаемостью равной $\varepsilon $ число силовых линий уменьшается в $\varepsilon $ раз, то векторная величина, равная:
\[\overline{D}=\varepsilon {\varepsilon }_0\overline{E}(2)\]будет оставаться неизменной при переходе из одного вещества в другое.
Определение вектора электрической индукции
Определение
Выражение (3) является наиболее общим определение вектора электрической индукции (вектора электрического смещения). Для большинства диэлектриков (исключением являются, например, сегнетоэлектрики) вектор поляризации пропорционален напряженности поля:
\[\overline{P}=\left(\varepsilon -1\right){\varepsilon }_0\overline{E}\left(4\right).\]В таком случае от формулы (3) мы приходим к определению вектора электрической индукции вида (2).
Название «вектор индукции» указывает на связь вектора $\overline{D}$ и явления электризации по влиянию (явление электростатической индукции).
Физический смысл вектора электрической индукции
Допустим, что в веществе, с диэлектрической проницаемостью равной $\varepsilon $ имеется очень тонкий вакуумный зазор, грани которого перпендикулярны направлению поля в точке рассмотрения (рис.1). В эту щель помещают точечный единичный положительный пробный заряд. Сила, с которой поле будет оказывать действие на этот пробный заряд, равна $\overline{D}.$
И так, вектор электрической индукции - это сила, которая действует на точечный единичный положительный заряд, находящийся в бесконечно узком зазоре, грани которого перпендикулярны направлению поля.
Силовые линии вектора $\overline{D}$ начинаются и заканчиваются на свободных зарядах. Величина $\overline{D}$ не зависит от диэлектрической проницаемости вещества.
В некоторых источниках вектор электрической индукции называют формальным, так как он равен сумме физических величин, относящихся к разным объектам к полю и к веществу (см формулу (3), где $\overline{E}$ - характеристика электрического поля; $\overline{P}$ - характеристика вещества). Тогда говорят, что вектор электрической индукции не имеет физического смысла.
Теорема Гаусса - Остроградского для поля в диэлектрике
Поток вектора электрической индукции равен алгебраической сумме свободных зарядов, которые находятся внутри рассматриваемой замкнутой поверхности:
\[\oint\nolimits_S{\overline{D}d\overline{S}=q\ \left(5\right).}\]По теореме (5) поток вектора $\overline{D}$ через любую замкнутую поверхность равен нулю, если внутри данной поверхности нет свободных зарядов. Заряды, находящиеся вне рассматриваемой поверхности на поток вектора $\overline{D}$, не влияют.
Примеры задач с решением
Пример 1
Задание. Чему равен вектор поляризации в некоторой точке однородного изотропного диэлектрика, если известен вектор электрической индукции в этой точке ($\overline{D}$)? Диэлектрическая проницаемость вещества равна $\varepsilon $.
Решение. За основу решения задачи примем определение вектора электрического смещения вида:
\[\overline{D}={\varepsilon }_0\overline{E}+\overline{P}\left(1.1\right).\]Выразим вектор поляризации из (1.1):
\[\overline{P}=\overline{D}-{\varepsilon }_0\overline{E}\ \left(1.2\right).\]Так как по условию рассматриваемый диэлектрик является однородным и изотропным, то:
\[\overline{D}=\varepsilon {\varepsilon }_0\overline{E}\ \left(1.3\right),\]следовательно:
\[\overline{E}=\frac{\overline{D}}{\varepsilon {\varepsilon }_0}\left(1.4\right).\]Подставим правую часть формулы (1.4) вместо $\overline{E}$ в уравнение (1.2), имеем:
\[\overline{P}=\overline{D}-{\varepsilon }_0\frac{\overline{D}}{\varepsilon {\varepsilon }_0}=\left(1-\frac{1}{\varepsilon }\right)\overline{D}.\]Ответ. $\overline{P}=\left(1-\frac{1}{\varepsilon }\right)\overline{D}$
Пример 2
Задание. Между двумя бесконечными заряженными пластинами, несущими одинаковые по величине, но противоположные по модулю заряды поместили пластину из диэлектрика. Пластина сторонних зарядов не имеет. Каков поток вектора электрической индукции через поверхность, которая изображена на рис.2?
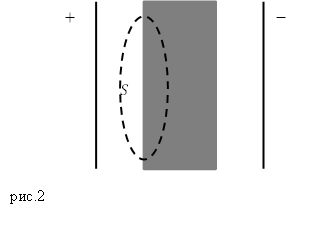
Решение. В соответствии с теоремой Гаусса поток вектора электрической индукции равен алгебраической сумме свободных зарядов, которые находятся внутри выделенной замкнутой поверхности (рис.2). Так как по условию задачи свободных зарядов между пластинами и в диэлектрике нет, то поток вектора $\overline{D}$ будет равен нулю:
\[\oint\nolimits_S{\overline{D}d\overline{S}=0\ .}\]Ответ. $\oint\nolimits_S{\overline{D}d\overline{S}=0\ }$
Читать дальше: давление идеального газа.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Статьи по теме
Поможем выполнить
любую работу
