Задание. Вычислите вектор Пойнтинга для стоячей электромагнитной волны.
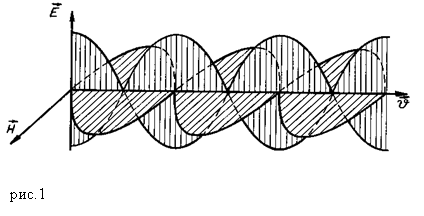
Колебания полей в стоячей электромагнитной волне можно представить при помощи формул:
\[\left\{ \begin{array}{c}
E=2E_0{\cos \left(kx-\frac{{\varphi }_E}{2}\right){\sin \left(\omega t-\frac{{\varphi }_E}{2}\right)\ }\ } \\
H=2H{\cos \left(kx-\frac{{\varphi }_H}{2}\right){\sin \left(\omega t-\frac{{\varphi }_H}{2}\right)\ }\ } \end{array}
\right.\left(1.1\right),\]
где ${\varphi }_E=2\pi \frac{2l}{\lambda }+?$ и ${\varphi }_H=2\pi \frac{2l}{\lambda }+\eta $\textit{ } - запаздывание по фазе отраженной волны соответствующих полей; $?$ и $\eta $ - изменения фазы при отражении, они равны нулю или $\pi ;;$ $l$ - для свободных волн расстояние между излучателем и отражающей поверхностью.
Решение.Прежде всего, введем обозначения:
\[\left\{ \begin{array}{c}
E_1=2E_0{cos \left(kx-\frac{{\varphi }_E}{2}\right),\ } \\
H_1=2H{cos \left(kx-\frac{{\varphi }_H}{2}\right)\ } \end{array}
\right.\left(1.2\right).\]
Тогда заданную систему уравнений (1.1) можно переписать как:
\[\left\{ \begin{array}{c}
E={E_1 {\sin \left(\omega t-\frac{{\varphi }_E}{2}\right)\ }\ } \\
H={H_1 {\sin \left(\omega t-\frac{{\varphi }_H}{2}\right)\ }\ } \end{array}
\right.\left(1.3\right),\]
где амплитуды $E_1$ и $H_1$ не зависят от времени. Предположим, что $?=\pi ,\ $тогда $\eta =0$ в результате имеем:
\[\left\{ \begin{array}{c}
E={E_1 {\sin \left(\omega t-\frac{2\pi \frac{2l}{\lambda }+\pi \ }{2}\right)=E_1{\cos \left(\omega t-\frac{2\pi l}{\lambda }\right),\ }\ }\ } \\
H={H_1 {\sin \left(\omega t-\frac{2\pi \frac{2l}{\lambda }}{2}\right)=\ }\ }H_1{\sin \left(\omega t-\frac{2\pi l}{\lambda }\right)\ }. \end{array}
\right.\left(1.3\right),\]
Для электромагнитной волны, в которой $\overline{E}\bot $ $\overline{H,}\ $следовательно:
\[S=EH\left(1.4\right)\]
получаем:
\[S=E_1{cos \left(\omega t-\frac{2\pi l}{\lambda }\right)\cdot \ }H_1{sin \left(\omega t-\frac{2\pi l}{\lambda }\right)\ }=\frac{E_1H_1}{2}{\sin \left(2\omega t-\frac{4\pi l}{\lambda }\right)\ }.\]
Ответ. $S=\frac{E_1H_1}{2}{\sin \left(2\omega t-\frac{4\pi l}{\lambda }\right)\ }$











