Дифракционной решеткой называют оптический прибор, работа которого основывается на явлении дифракции волн.
Амплитудная дифракционная решетка
С его помощью можно проводить периодическую модуляцию световой волны по амплитуде и фазе. Дифракционная решётка предназначена для спектрального анализа, нахождения длин волн.
Амплитудные дифракционные решетки
Рассмотрим одномерную дифракционную решетку, состоящую из $N$ параллельных равноотстоящих щелей (ширина щели равна $a$) и непрозрачных участков. Период решетки обозначим $d$ (рис.1). Свет, попадающий на решетку, будем считать монохроматическим.
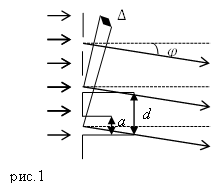
В случае нормального падения света на амплитудную решетку разность хода ($\Delta $) для соседних прозрачных участков составляет:
\[\Delta =d\ sin\ \varphi \left(1\right).\]Сдвиг по фазе при этом ($\delta $) будет:
\[\delta =\frac{2\pi \Delta }{\lambda }=\frac{2\pi dsin\varphi }{\lambda }=2\pi \cdot d\cdot u\left(2\right),\]где $u=\frac{sin\varphi }{\lambda }$ - величина, названная пространственной частотой;$\ \lambda $ - длина волны падающего света. Световое поле найдем как:
\[E=E_1+\frac{E_1}{e^{i\delta }}+\frac{E_1}{e^{i2\delta }}+\frac{E_1}{e^{i3\delta }}+\dots =E_1\frac{1-e^{-2iN\delta }}{1-e^{-i\delta }}\left(3\right),\]где $E_1$ - амплитуда поля, после прохождения одной щели; выражение (3) представляет собой геометрическую прогрессию. Угловое распределение интенсивности света, который дифрагировала через решетку:
\[\ I=I_0I_1I_N=I_0{\left[\frac{{\sin \left(\pi au\right)\ }}{\pi au}\right]}^2{\left[\frac{{\sin \left(N\pi du\right)\ }}{\pi du}\right]}^2\left(4\right),\]где $I_0$ - интенсивность падающего света, $I_1$ - интенсивность прошедшего света, (для одной щели). $I_N$ - интенсивность света при наложении нескольких лучей. Все пучки света обладают равной интенсивностью.
Интенсивность света после дифракционной решетки
Максимальная интенсивность света после дифракции получается в направлениях:
\[dsin{\varphi }_m=m\lambda \ или\ \frac{sin{\varphi }_m}{\lambda }=u=\frac{m}{d},\ m=0,\ \pm 1,\pm 2\dots \left(5\right),\]то у функции $I_N\ $ числитель и знаменатель будут равны нулю.
Принимая во внимание:
\[{\mathop{\lim }_{\delta \to 0} \left|\frac{sinN\delta }{sin\delta }\right|\ }=N\left(6\right),\]имеем:
\[I_m=I_0N^2d^2\frac{{sin}^2(\frac{\pi ma}{d})}{{(\pi ma)}^2}=\frac{N^2}{m^2}\frac{I_0d^2}{{\pi }^2a^2}{sin}^2\left(\frac{\pi ma}{d}\right)\left(7\right).\]Если будет выполняться условие главных максимумов (условие 5), то интенсивность света, совершающего дифракцию на решетке, которая имеет $N$ щелей, растет в $N^2$ раз. Данный результат получен в результате многолучевой интерференции световых лучей, прошедших сквозь регулярную структуру. Выражение (7) говорит о том, что интенсивность главных максимумов уменьшается с увеличением порядка максимума. По мимо этого, $I_m\sim \frac{d}{a}$ -это целое число. Главные максимумы порядков $\frac{d}{a}$, 2$\frac{d}{a}$, ..., совпадают с минимумами дифракции на одной щели, получаем, что их интенсивность равна нулю. Например, при $\frac{d}{a}=2$ прозрачная и непрозрачная части взаимно равны, при этом спектр решетки обладает исключительно главными максимумами нулевого и нечетных порядков.
Дифракционная решетка, имеющая $N$ щелей, порождает на отрезках между главными максимумами $(N-1)$ минимум и $(N-2)$ добавочных максимума. При увеличении числа $N$ дополнительными максимума обычно пренебрегают, так как они имеют малую интенсивность.
При наклонном падении волны на решетку не равна нулю пространственная частота:
\[u=\frac{{{\sin \varphi \ }}_0}{\lambda }\left(8\right).\]При этом условие главных максимумов принимает вид:
\[d\left(sin\varphi -sin{\varphi }_0\right)=m\lambda \left(9\right).\]Свойства амплитудной дифракционной решетки
Свойства дифракционной решетки характеризуют при помощи следующих параметров:
- Угловой дисперсии (D): \[D=\frac{\delta \varphi }{\delta \lambda }=\frac{m}{dcos\varphi }\left(10\right).\]
- Разрешающей способности (R): \[R=\frac{\lambda }{\delta {\lambda }_{min}}=mN\left(11\right),\]
где $\delta {\lambda }_{min}$ - минимальная разность длин волн, которая разрешается решеткой.
- Дисперсионной областью $\Delta \lambda $: \[\Delta \lambda =\frac{\lambda }{m}\left(12\right).\]
На практике амплитудные дифракционные решетки применяют редко, так как они дают слабую светосилу рабочих максимумов. Основная доля энергии света падает на центральный максимум ($m=0$), который не интересен при изучении спектра.
Примеры задач с решением
Задание. Какова постоянная дифракционной решетки ($d$), если угловая дисперсия ее равна $D$ для длины волны $\lambda $ для спектра порядка $m$?
Решение. Сделаем рисунок.
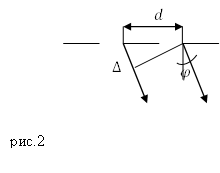
За основу решения задачи примем определение угловой дисперсии в виде:
\[D=\frac{\delta \varphi }{\delta \lambda }=\frac{m}{dcos\varphi }\left(1.1\right).\]Запишем условие максимума при дифракции:
\[d{\sin \varphi =m\lambda \ \left(1.2\right).\ }\]Из выражения (1.1) выразим $cos\varphi $:
\[cos\varphi =\frac{m}{Dd}\left(1.3\right).\]Уравнение (1.2) даст нам ${\sin \varphi \ }$:
\[{\sin \varphi =\frac{m\lambda }{d}\ \left(1.4\right).\ }\]Из формул (1.3) и (1.4) найдем:
\[tg\ \varphi =\lambda D\to \varphi =arc\ tg\ \left(\lambda D\right)\left(1.5\right).\]Постоянную дифракционной решетки найдем как:
\[d=\frac{m\lambda }{{\rm sin}(arc\ tg\ \left(\lambda D\right))}.\]Ответ. $d=\frac{m\lambda }{{\rm sin}(arc\ tg\ \left(\lambda D\right))}$
Задание. Какова разрешающая сила дифракционной решетки, если известна угловая дисперсия ($D$) данной решетки для волны $\lambda $? Длина рассматриваемой решетки $l$.
Решение. Основу для решения задачи составят выражения:
\[D=\frac{m}{dcos\varphi }\left(2.1\right).\] \[R=\frac{\lambda }{\delta {\lambda }_{min}}=mN\left(2.2\right).\]Из формулы (2.1) выразим $m$, имеем:
\[m=d\cdot D\ cos\varphi \ \left(2.3\right).\]Результат (2.3) подставим в (2.2):
\[R=d\cdot D\ cos\varphi \cdot N\ \left(2.4\right).\]Число штрихов на решетке можно найти, если известна ее длина как:
\[l=Nd\to N=\frac{l}{d}\left(2.5\right).\]Учитывая (2.5) формулу (2.4) представим в виде:
\[R=d\cdot D\ cos\varphi \cdot \frac{l}{d}=D\ cos\varphi \cdot l\left(2.6\right).\]Считая углы дифракции малыми, можно положить, что:
\[cos\varphi \approx 1,\]тогда разрешающая сила решетки равна:
\[R\approx D\ \cdot l.\]Ответ. $R\approx D\ \cdot l$
Читать дальше: бозоны и фермионы.










