Формула скорости свободного падения в физике
Формула скорости свободного падения
Ускорение и скорость при свободном падении
Движение тела около поверхности Земли под воздействием силы тяжести называют свободным падением. При исследовании свободного падения тела, обычно силы сопротивления воздуха не учитывают.
Напомним, что величина ускорения свободного падения около поверхности Земли вычисляется как:
\[g=\gamma \frac{M}{({R+h)}^2}\left(1\right),\]
где $\gamma =6,67\cdot {10}^{-11}\frac{Н\cdot м^2}{{кг}^2}$- гравитационная постоянная; $M$ - масса Земли; $R$ - радиус Земли.
Если расстояние, с которого падает тело много меньше, чем радиус Земли ($\ h\ll R$), то ускорение свободного падения считают постоянной величиной, равной:
\[g=\gamma \frac{M}{R^2}\approx 9,8\ (\frac{м}{с^2})\left(2\right).\]
Кинематическое уравнение скорости при свободном падении
Свободное падение происходит с постоянным ускорением, что было установлено еще Галилеем, поэтому скорость в кинематике определяет уравнение для равнопеременного движения:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(3\right).\]
Уравнение (3) показывает изменение вектора скорости $\overline{v}\left(t\right),$ где ${\overline{v}}_0$ - начальная скорость движения тела.
Используя это уравнение, и зная начальные условия движения тела можно найти скорость тела относительно избранной системы отсчета для любого момента времени.
Скорость тела, брошенного под углом к горизонту
Допустим, что тело бросили под углом $\alpha $ к горизонту. Ось X системы координат направим горизонтально, ось Y перпендикулярно горизонту вверх, тогда начальные условия движения для скорости данного тела запишем как:
\[\left\{ \begin{array}{c}
v_x\left(t=0\ \right)=v_0{\cos \alpha ,\ } \\
v_y\left(t=0\ \right)=v_0{\sin \alpha \ } \end{array}
\right.\left(4\right).\]
Это означает, что тело бросили под углом $\alpha $ к горизонту с начальной скоростью ${\overline{v}}_0$. При этом проекции уравнения (3) дадут нам систему уравнений:
\[\left\{ \begin{array}{c}
v_x\left(t\right)=v_0{\cos \alpha ,\ } \\
v_y\left(t\right)=v_0{\sin \alpha -gt\ } \end{array}
\right.\left(5\right).\]
Формула скорости при свободном падении тела из состояния покоя
Начальные условия для скорости движения для тела, которое падает из состояния покоя, запишем так:
\[\left\{ \begin{array}{c}
v_x\left(t=0\ \right)=0, \\
v_y\left(t=0\ \right)=0 \end{array}
\right.\left(6\right).\]
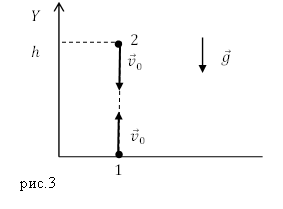
В таком случае выражение (3) в проекции на ось Y, которую выберем вдоль направления движения (рис.1), тела будет выглядеть как:
\[\left\{ \begin{array}{c}
v_y=-gt \end{array}
\right.\left(7\right).\]
В момент падения скорость тела при свободном его падении с высоты $h$ равна:
\[v_{pad}=-\sqrt{2gh}\left(8\right).\]
Знак минус в формуле (8) означает, что скорость падения направлена против нашей оси Y.
Отметим, что тело, брошенное вертикально вверх движется до максимальной высоты подъема столько же времени, сколько оно потом падает с этой высоты до точки бросания.
Примеры задач с решением
Пример 1
Задание. Тело бросили вертикально вверх. Оно вернулось в точку бросания через $t'$ секунд. Какова начальная скорость тела?\textit{}
Решение. Сделаем рисунок.
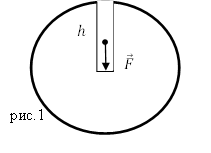
Запишем уравнение для скорости движения тела в векторном виде:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(1.1\right).\]
Найдем проекцию этого уравнения на ось Y:
\[v=v_0-gt\ \left(1.2\right).\]
В точке максимального подъема скорость тела равна нулю, следовательно:
\[0=v_0-g{t\ }_{pod}\to v_0=g{t\ }_{pod}\left(1.3\right).\]
Принимая во внимание, что время подъема равно времени спуска при отсутствии сил трения, имеем:
\[{t\ }_{pod}=\frac{t'}{2}\left(1.4\right).\]
Подставим (1.4) в (1.3), имеем:
\[v_0=g\frac{t'}{2}.\]
Ответ. $v_0=g\frac{t'}{2}$
Пример 2
Задание. Одно тело бросили вертикально вверх с начальной скоростью равной $v_0.$ В этот же момент времени вертикально вниз с начальной скоростью $v_0$ бросили второе тело. Высота, с которой бросили это тело равно высоте максимального подъема первого тела. Какова скорость первого и второго тел в момент встречи этих двух тел? Тела считайте материальными точками, сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
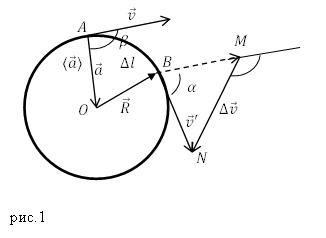
За основу решения задачи примем уравнение для скорости движения тела в поле тяжести Земли:
\[\overline{v}\left(t\right)={\overline{v}}_0+\overline{g}t\ \left(2.1\right).\]
Для первого тела уравнение (2.1) в проекции на ось Y будет иметь вид:
\[v_1=v_0-gt\ \left(2.2\right).\]
Уравнение скорости второго тела при его падении выглядит как:
\[{-v}_2=-v_0-gt\ \left(2.3\right).\]
Для решения задачи будем использовать кинематическое уравнение для перемещения тела с постоянным ускорением:
\[\overline{s}\left(t\right)={\overline{s}}_0+{\overline{v}}_0t+\frac{\overline{g}t^2}{2}\left(2.4\right).\]
В проекции на ось Y это уравнение для первого тела, поднимающегося вверх, даст выражение:
\[y_1=v_0t-\frac{gt^2}{2}\left(2.5\right).\]
Для второго тела при его падении в проекции на ось Y (2.4) запишется как:
\[y_2=h-v_0t-\frac{gt^2}{2}\left(2.6\right).\]
Найдем время встречи тел ($t'$) из системы уравнений (2.5) и (2.6), учитывая, что при встрече тел $y_1=y_2$:
\[v_0t'-\frac{g{t'}^2}{2}=h-v_0t'-\frac{g{t'}^2}{2}\to 0=h-2v_0t'\to t'=\frac{h}{2v_0}\left(2.7\right).\]
Подставим время $t'$ в уравнение (2.2) получим скорость первого тела в момент встречи:
\[v_1=v_0-g\frac{h}{2v_0}\left(2.8\right).\]
Найдем высоту $h$, на которую способно подняться первое тело. Для этого найдем время подъема тела, зная, что в точке максимального подъема скорость тела равна нулю:
\[v_1=v_0-gt=0\to t_{pod}=\frac{v_0}{g}\left(2.9\right).\]
Высота подъема, она же высота с которой бросили второе тело найдётся из уравнения (2.5), если в него подставить $t_{pod}$:
\[y_1=h=v_0t-\frac{g{t_{pod}}^2}{2}=v_0\frac{v_0}{g}-\frac{g}{2}\frac{v^2_0}{g^2}=\frac{v^2_0}{2g}\left(2.10\right).\]
Подставляя вместо $h$ правую часть уравнения (2.10) в формулу (2.8) получим скорость движения первого тела в его момент встречи со вторым телом:
\[v_1=v_0-g\frac{v^2_0}{2g}\frac{1}{2v_0}=\frac{3}{4}v_0.\]
Используя уравнение (2.3), подставляя в нее время встречи тел ($t'$) из (2.7), учитывая (2.10) получим скорость движения второго тела в момент встречи:
\[v_2=v_0+gt=v_0+g\frac{1}{2v_0}\frac{v^2_0}{2g}=v_0+\frac{v_0}{4}=\frac{5}{4}v_0.\]
Ответ. $v_1=\frac{3}{4}v_0,$ $v_2=\frac{5}{4}v_0$
Читать дальше: формула ускорения свободного падения.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 463 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!













