Период - это минимальное время, за которое совершается одно полное колебательное движение.
Формула периода колебаний пружинного маятника
Обозначают период буквой $T$.
\[T=\frac{\Delta t}{N}\left(1\right),\]где $\Delta t$ - время колебаний; $N$ - число полных колебаний.
Уравнение колебаний пружинного маятника
Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k\ $(рис.1). Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести. Колебания пружинного маятника возникают, когда систему выводят из состояния равновесия, например, слегка дополнительно растянув пружину, после этого маятник предоставляют самому себе.
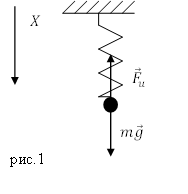
Допустим, что масса пружины мала в сравнении с массой груза, при описании колебаний ее учитывать не будем. Началом отсчета будем считать точку на оси координат (X), которая совпадает с положением равновесия груза. В этом положении пружина уже имеет удлинение, которое обозначим $b$. Растяжение пружины происходит из-за действия на груз силы тяжести, следовательно:
\[mg=kb\ \left(2\right).\]Если груз смещают дополнительно, но закон Гука еще выполняется, то сила упругости пружины становится равна:
\[F_u=-k\left(x+b\right)\left(3\right).\]Ускорение груза запишем, помня, что движение происходит по оси X, как:
\[a=\frac{d^2x}{dt^2}=\ddot{x\ }\left(4\right).\]Второй закон Ньютона для груза принимает вид:
\[m\ddot{x}=-k\left(x+b\right)+mg\ \left(5\right).\]Учтем равенство (2), формулу (5) преобразуем к виду:
\[m\ddot{x}=-kx-kb+mg=-kx-mg+mg=-kx\ \left(6\right).\]Если ввести обозначение: ${\omega }^2_0=\frac{k}{m}$, то уравнение колебаний запишем как:
\[\ddot{x}+{\omega }^2_0x=0\left(7\right),\]где ${\omega }^2_0=\frac{k}{m}$ - циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:
\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(8\right),\]где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ - амплитуда колебаний; ${(\omega }_0t+\varphi )$ - фаза колебаний; $\varphi $ и ${\varphi }_1$ - начальные фазы колебаний.
Формулы периода колебаний пружинного маятника
Мы получили, что колебания пружинного маятника описывается функцией косинус или синус. Это периодические функции, значит, смещение $x$ будет принимать равные значения через определенные одинаковые промежутки времени, которые называют периодом колебаний. Обозначают период буквой T.
Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($\nu $):
\[T=\frac{1}{\nu }\left(9\right).\]Период связан с циклической частотой колебаний как:
\[T=\frac{2\pi }{{\omega }_0}\left(10\right).\]Выше мы получали для пружинного маятника ${\omega }_0=\sqrt{\frac{k}{m}}$, следовательно, период колебаний пружинного маятника равен:
\[T=2\pi \sqrt{\frac{m}{k}}\ \left(11\right).\]Формула периода колебаний пружинного маятника (11) показывает, что $T$ зависит от массы груза, прикрепленного к пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Данное свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, появляется зависимость колебаний от амплитуды. Подчеркнем, что формула (11) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.
Примеры задач на период колебаний
Задание. Пружинный маятник совершил 50 полных колебаний за время равное 10 с . Каков период колебаний маятника? Чему равна частота этих колебаний?
Решение. Так как период - это минимальное время необходимое маятнику для совершения одного полного колебания, то найдем его как:
\[T=\frac{\Delta t}{N}\left(1.1\right).\]Вычислим период:
\[T=\frac{10}{50}=0,2\ \left(с\right).\]Частота - величина обратная периоду, следовательно:
\[\nu =\frac{1}{T}\left(1.2\right).\]Вычислим частоту колебаний:
\[\nu =\frac{1}{0,2}=5\ \left(Гц\right).\]Ответ. $1)\ T=0,2$ с; 2) 5Гц
Задание.Две пружины, имеющие коэффициенты упругости $k_1$ и $k_2$ соединены параллельно (рис.2), к системе присоединен груз массы $M$. Каков период колебаний полученного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука?
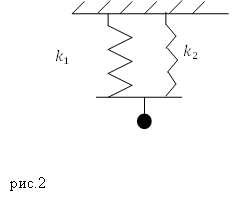
Решение. Воспользуемся формулой для вычисления периода колебаний пружинного маятника:
\[T=2\pi \sqrt{\frac{M}{k}}\ \left(2.1\right).\]При параллельном соединении пружин результирующая жесткость системы находится как:
\[k=k_1{+k}_2\left(2.2\right).\]Это означают, что вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:
\[T=2\pi \sqrt{\frac{M}{k_1{+k}_2}}.\]Ответ. $T=2\pi \sqrt{\frac{M}{k_1{+k}_2}}$
Читать дальше: формула плеча силы.










