Закон Архимеда, теория и онлайн калькуляторы
Закон Архимеда
Если тело погрузить в жидкость, то на это тело со всех сторон действуют силы давления жидкости. Эти силы направлены перпендикулярно поверхности тела в каждой его точке. Если бы все силы, действующие на тело, были одинаковы по величине, то оно испытывало бы только всестороннее сжатие. Однако мы знаем, что при увеличении глубины гидростатическое давление увеличивается, следовательно, силы давления, которые приложены к нижним частям тела больше, чем силы, которые действуют на тело вверху.
Если заменить все силы давления, которые приложены к телу, находящемуся в жидкости, одной результирующей силой, то эта сила будет направлена вверх. В этой связи ее назвали выталкивающей силой. По-другому ее называют силой Архимеда (${\overline{F}}_A$). Именно Архимед отметил факт ее существования и определил, как ее вычислить.
Сила Архимеда оказывает свое действие на тела не только в жидкостях, но и газах, там, где существует гиростатическое давление.
Благодаря действию силы Архимеда всплывают тела в жидкости, могут летать воздушные шары. Из-за выталкивающей силы вес каждого тела в жидкости меньше, чем в воздухе. Уменьшение веса тела произойдет, если перенести тело из вакуума в любой газ. Если вес тела в вакууме равен $P$, то его вес в жидкости или газе равен:
\[P'=P-F_A\left(1\right).\]
Формулировка закона Архимеда
Сила Архимеда, оказывающая действие на тело, погруженное в жидкость (или газ), равна весу жидкости (или газа), в объеме вытесненной (вытесненным) этим телом.
Сила выталкивания не зависит от вещества, из которого состоит тело, как от него не зависит давление окружающих тело слоев жидкости. Пусть погруженное в жидкость тело состоит из этой же жидкости. Данное жидкое тело, как и другая часть окружающей его жидкости, будет находиться в равновесии. Это означает, что приложенная к нему сила Архимеда, уравновешивается силой тяжести:
\[F_A=m_gg\ \left(2\right),\]
где $m_g={\rho }_gV$ - масса жидкости в объеме рассматриваемого тела; ${\rho }_g$ - плотность жидкости. Но, сила тяжести $(m_gg)$ равна весу вытесненной жидкости $P$, следовательно:
\[F_A=P\left(3\right).\]
Это означает, что выражение (2) можно переписать в виде:
\[F_A={\rho }_gV\ g\left(4\right),\]
где $V$- объем вытесненной телом жидкости. Если тело находится в жидкости целиком, то это объем тела. Если тело частично погружено в жидкость, то V - часть тела, находящаяся в жидкости.
Закон Архимеда в виде (4) выполняется и для газов.
Закон Архимеда на сегодняшний день можно формулировать так: На любое тело, которое погружено в жидкость (газ), находящуюся в состоянии равновесия, действует со стороны жидкости (газа) сила выталкивания, равная произведению плотности вещества в котором находится тело, на ускорение свободного падения и на объем погруженной части тела.
Примеры задач на закон Архимеда
Пример 1
Задание. Чему равна сила Архимеда, если тело плавает на границе раздела двух жидкостей с разными плотностями?
Решение. Если тело плавает на границе раздела двух жидкостей, имеющих разные плотности, то силу Архимеда найдем как:
\[F_A=g\left[{\rho }_1V_1+{\rho }_2V_2\right]\ ,\]
где ${\rho }_1$ - плотность первой жидкости; ${\rho }_2$ - плотность второй жидкости; $V_1$ - объем тела, находящийся в первой жидкости; $V_2$ - объем тела во второй жидкости.
Пример 2
Задание. Вес тела в воздухе равен $P_1$, его же вес в жидкости, плотность которой равна ${\rho }_g$, равен $P_2$. Какова плотность тела ($\rho $)?
Решение. Сделаем рисунок.
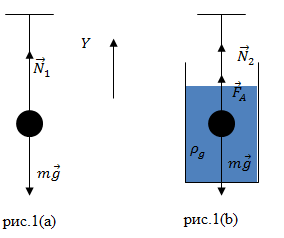
Вес тела по третьему закону Ньютона равен по величине силе натяжения нити и направлен в противоположную сторону: ($\overline{N}=-\overline{P}$). Сила натяжения нити на нашем рисунке обозначается буквой N. В соответствии со вторым законом Ньютона сила натяжения нити в воздухе (рис.1(а)) равна:
\[{\overline{N}}_1=-m\overline{g}\to Y:\ N_1=mg\ \to P_1=mg\left(2.1\right).\]
Запишем второй закон Ньютона для сил, которые действуют на тело во втором случае (рис.1(b)):
\[m\overline{g}+{\overline{N}}_2+{\overline{F}}_A=0\ \left(2.2\right).\]
В проекции на ось Y выражения (2.2) имеем:
\[F_A+N_2-mg=0\ \left(2.3\right).\]
Масса рассматриваемого тела равна:
\[m=\rho V\ \left(2.4\right),\]
где $V$ - объем тела. Сила Архимеда, действующая на тело (рис.1(b)):
\[F_A={\rho }_gVg\ \left(2.5\right).\]
Выразим вес тела из (2.3), учтем выражения (2.4) и (2.5):
\[N_2=\rho Vg-{\rho }_gVg=P_2\ \left(2.6\right).\]
Найдем отношение выражений (2.6) к (2.1):
\[\frac{P_2}{P_1}=\frac{\rho Vg-{\rho }_gVg\ }{\rho Vg}=1-\frac{{\rho }_g}{\rho }\left(2.7\right).\]
Из формулы (2.7) получим выражение для плотности тела:
\[\rho =\frac{{\rho }_g}{P_1-P_2}P_1.\]
Ответ. $\rho =\frac{{\rho }_g}{P_1-P_2}P_1$
Читать дальше: формула второго закона Ньютона.
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in
/var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line
20

Мы помогли уже 4 454 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!











