Начальная фаза колебаний - это параметр, который совместно с амплитудой колебаний определяет начальное состояние колебательной системы. Величину начальной фазы задают в начальных условиях, то есть при $t=0$ c.
Начальная фаза колебаний
Рассмотрим гармонические колебания некоторого параметра $\xi $. Гармонические колебания описываются уравнением:
\[\xi =A{\cos ({\omega }_0t+\varphi )\ }\ \left(1\right),\]где $A={\xi }_{max}$ - амплитуда колебаний; ${\omega }_0$ - циклическая (круговая) частота колебаний. Параметр $\xi $ лежит в пределах $-A\le \xi \le $+A.
Определение фазы колебаний
Весь аргумент периодической функции (в данном случае косинуса:$\ ({\omega }_0t+\varphi )$), описывающей колебательный процесс, называют фазой колебаний. Величина фазы колебаний в начальный момент времени, то есть при $t=0$, ($\varphi $)- носит название начальной фазы. Устоявшегося обозначения фазы нет, у нас начальная фаза обозначена $\varphi $. Иногда, чтобы подчеркнуть, что начальная фаза относится к моменту времени $t=0$ к букве, обозначающей начальную фазу, добавляют индекс 0, пишут, например, ${\varphi }_0.$
Единицей измерения начальной фазы является единица измерения угла - радиан (рад) или градус.
Начальная фаза колебаний и способ возбуждения колебаний
Допустим, что при $t=0$ смещение системы от положения равновесия равно ${\xi }_0$, а начальная скорость ${\dot{\xi }}_0$. Тогда уравнение (1) принимает вид:
\[\xi \left(0\right)=A{\cos \varphi =\ }{\xi }_0\left(2\right);;\] \[\ \frac{d\xi }{dt}=-A{\omega }_0{\sin \varphi =\ }{\dot{\xi }}_0\to -A{\sin \varphi =\frac{{\dot{\xi }}_0}{{\omega }_0}\ }\ \left(3\right).\]Возведем в квадрат оба уравнения (2) и сложим их:
\[{\xi }^2_0+{\left(\frac{{\dot{\xi }}_0}{{\omega }_0}\right)}^2=A^2\left(4\right).\]Из выражения (4) имеем:
\[A=\sqrt{{\xi }^2_0+{\left(\frac{{\dot{\xi }}_0}{{\omega }_0}\right)}^2\ }\left(5\right).\]Разделим уравнение (3) на (2), получим:
\[tg\ \varphi =-\frac{{\dot{\xi }}_0}{{{\xi }_0\omega }_0}\left(6\right).\]Выражения (5) и (6) показывают, что начальная фаза и амплитуда зависят от начальных условий колебаний. Это значит, что амплитуда и начальная фаза зависят от способа возбуждения колебаний. Например, если груз пруженного маятника отклоняют от положения равновесия и на расстояние $x_0$ и отпускают без толчка, тогда уравнением движения маятника является уравнение:
\[x=A{\cos \left({\omega }_0t+\varphi \right)\ }(7)\]с начальными условиями:
\[x\left(0\right)=x_0;;\ \dot{x}\left(0\right)=0\ \left(8\right).\]При таком возбуждении колебания пружинного маятника можно описывать выражением:
\[x=x_0{\cos \left({\omega }_0t\right)\left(9\right).\ }\]Сложение колебаний и начальная фаза
Тело, совершающее колебания, способно принимать участие в нескольких колебательных процессах одновременно. В таком случае возникает необходимость выяснить, каким будет результирующее колебание.
Допустим, что два колебания с равными частотами происходят по одной прямой. Уравнением результирующих колебаний будет выражение:
\[\xi ={\xi }_1+{\xi }_2=A{\cos \left({\omega }_0t+\varphi \right),\ }\]тогда амплитуда суммарного колебания равна:
\[A=\sqrt{A^2_1+A^2_2+2A_1A_2{\cos \left({\varphi }_2-{\varphi }_1\right)\ }\left(10\right),}\]где $A_1$; $A_2$ - амплитуды складывающихся колебаний; ${\varphi }_2;;{\varphi }_1$ - начальные фазы суммирующихся колебаний. При этом начальную фазу полученного колебания ($\varphi $) вычисляют, применяя формулу:
\[tg\ \varphi =\frac{A_1{\sin {\varphi }_1+A_2{sin {\varphi }_2\ }\ }}{A_1{\cos {\varphi }_1+A_2{cos {\varphi }_2\ }\ }}\left(11\right).\]Уравнение траектории точки, которая принимает участие в двух взаимно перпендикулярных колебаниях с амплитудами $A_1$и $A_2$ и начальными фазами ${\varphi }_2и{\varphi }_1$:
\[\frac{x^2}{A^2_1}+\frac{y^2}{A^2_2}-\frac{2xy}{A_1A_2}{\cos \left({\varphi }_2-{\varphi }_1\right)\ }={sin}^2\left({\varphi }_2-{\varphi }_1\right)\left(12\right).\]В случае равенства начальных фаз составляющих колебаний уравнение траектории имеет вид:
\[y=\frac{A_2}{A_1}x\ или\ y=-\frac{A_2}{A_1}x\ \left(13\right),\]что говорит о движении точки по прямой линии.
Если разность начальных фаз складываемых колебаний составляет $\Delta \varphi ={\varphi }_2-{\varphi }_1=\frac{\pi }{2},$ уравнением траектории становится формула:
\[\frac{x^2}{A^2_1}+\frac{y^2}{A^2_2}=1\left(14\right),\]что означает, траектория движения эллипс.
Примеры задач с решением
Задание. Колебания пружинного осциллятора возбуждены толчком из положения равновесия, при этом грузу сообщают мгновенную скорость, равную $v_0$. Запишите начальные условия для такого колебания и функцию $x(t)$, описывающую данные колебания.
Решение. Сообщение грузу пружинного маятника мгновенной скорости равной $v_0$ означает, что при описании его колебаний с помощью уравнения:
\[x=A{\cos \left({\omega }_0t+\varphi \right)\ }(1.1)\]начальными условиями будут:
\[x\left(0\right)=0;;\ \dot{x}\left(0\right)=v_0\left(1.2\right).\]Подставим в выражение (1.1) $t=0$, имеем:
\[x=A{\cos \left(\varphi \right)\ }=0\ \left(1.3\right).\]Так как $A\ne 0$, то ${\cos \left(\varphi \right)\ }=0\to \varphi =\pm \frac{\pi }{2}.$
Возьмем первую производную $\frac{dx}{dt}$ подставим момент времени $t=0$:
\[\dot{x}\left(0\right)=-A{\omega }_{0\ }{\sin \left(\varphi \right)\ }=v_0\to A=\frac{v_0}{{\omega }_{0\ }}\ \left(1.4\right).\]Из (1.4) следует, что начальная фаза получается $\varphi =-\frac{\pi }{2}.$ Подставим, полученную начальную фазу и амплитуду в уравнение (1.1):
\[x=\frac{v_0}{{\omega }_{0\ }}{\cos \left({\omega }_0t-\frac{\pi }{2}\right)\ }=\frac{v_0}{{\omega }_{0\ }}{\sin (\ }{\omega }_0t).\]Ответ. $x(t)=\frac{v_0}{{\omega }_{0\ }}{\sin (\ }{\omega }_0t)$
Задание. Два колебания одного направления складываются. Уравнения этих колебаний имеют вид: $x_1={\cos \pi (t+\frac{1}{6})\ };;\ x_2=2{\cos \pi (t+\frac{1}{2})\ }$. Какова начальная фаза полученного колебания?
Решение. Запишем уравнение гармонических колебаний по оси X:
\[x=A{\cos \left({\omega }_0t+\varphi \right)\ }\left(2.1\right).\]Преобразуем заданные в условии задачи уравнения к этому же виду:
\[x_1={\rm cos}\left[\pi t+\frac{\pi }{6}\right];;\ x_2=2{\cos \left[\pi t+\frac{\pi }{2}\right](2.2).\ }\]Сравнивая уравнения (2.2) с (2.1) получим, что начальные фазы колебаний равны:
\[{\varphi }_1=\frac{\pi }{6};;\ {\varphi }_2=\frac{\pi }{2}.\]Изобразим на рис.1 векторную диаграмму колебаний.
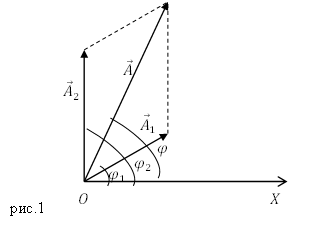
$tg\ \varphi $ суммарных колебаний можно найти из рис.1:
\[tg\ \varphi =\frac{A_1{\sin {\varphi }_1+A_2{sin {\varphi }_2\ }\ }}{A_1{\cos {\varphi }_1+A_2{cos {\varphi }_2\ }\ }}=\frac{{\sin \left(\frac{\pi }{6}\right)+2{\sin (\frac{\pi }{2})\ }\ }}{{\cos \left(\frac{\pi }{6}\right)+2{\cos (\frac{\pi }{2})\ }\ }}=2,87.\] \[\varphi =arctg\ \left(2,87\right)\approx 70,9{}^\circ \]Ответ. $\varphi =70,9{}^\circ $
Читать дальше: начальная фаза.










