Решение СЛАУ 3-его порядка методом Крамера, пример № 1
СЛАУ 3-его порядка: 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12
Условие
|
Решение системы линейных алгебраических уравнений методом Крамера
Для проверки ответов можете воспользоваться нашим онлайн сервисом - Решение системы линейных уравнений методом Крамера. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по математике и другим предметам!
Систему уравнений можно представить в матричной форме: Ax = B, где А - основная матрица (квадратная матрица), В - матрица свободных членов.
Теперь необходимо найти 4 определителя: определитель основной матрицы (определитель системы) и 3 определителя дополнительных матриц. Перед нахождением определителей советуем ознакомиться с теорией определителей матриц, а для нахождения определителей советуем использовать нашу программу - нахождение определителя матрицы.
Перепишем систему линейных алгебраических уравнений в матричную форму. Слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.
 |
|
|  |
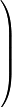Найдем определитель основной матрицы:
| Δ = |
| = | - 2 · 1 · 5 + 1 · 2 · 4 - 2 · 3 · 1 + 2 · 1 · 4 + 2 · 1 · 2 - 5 · 1 · 3 = -11 |
Определитель основной матрицы не равен нуля, значит система невырожденная.
Найдем определители 3 дополнительных матриц:
Дополнительная матрица получается из основной путем замены элементов одного из трех столбцов основной матрицы элементами матрицы свободных членов.
| Δ 1 = |
| = | - 1 · 1 · 5 - 1 · 2 · 3 - 2 · 1 · 1 - 2 · 1 · 3 + 2 · 1 · 1 - 5 · 1 · 1 = -22 |
| Δ 2 = |
| = | 2 · 1 · 5 + 1 · 2 · 4 - 2 · 3 · 3 - 2 · 1 · 4 + 2 · 3 · 2 - 5 · 1 · 3 = -11 |
| Δ 3 = |
| = | 2 · 1 · 3 + 1 · 1 · 4 - 1 · 3 · 1 + 1 · 1 · 4 + 1 · 1 · 2 + 3 · 1 · 3 = 22 |
Найдем решения системы алгебраических уравнений:
х1 = Δ1/Δ = 2
х2 = Δ2/Δ = 1
х3 = Δ3/Δ = -2
Вы поняли, как решать? Нет?
Другие примеры
- Решение СЛАУ 3-его порядка методом Крамера, пример № 10
- Решение СЛАУ 3-его порядка методом Крамера, пример № 11
- Решение СЛАУ 3-его порядка методом Крамера, пример № 12
- Решение СЛАУ 3-его порядка методом Крамера, пример № 2
Рассчитайте цену решения ваших задач
Калькулятор
стоимости
Решение контрольной
от 300 рублей
*
* Точная стоимость будет определена после загрузки задания для исполнителя