Решение СЛАУ 3-его порядка методом Гаусса, пример № 1

СЛАУ 3-его порядка: 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12
СЛАУ 4-ого порядка: 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12

Условие

 x 1 + 2x 2 + 3x 3   =   3
 3x 1 + 5x 2 + 7x 3   =   0
 x 1 + 3x 2 + 4x 3   =   1


Решение системы линейных алгебраических уравнений методом Гаусс

Для проверки ответов можете воспользоваться нашим онлайн сервисом - Решение системы линейных уравнений методом Гаусса. Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются элементарными преобразованиями матрицы. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по математике и другим предметам!

Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 3 × 4, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.


1
2
3
3
5
7
1
3
4
3
0
1

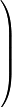Проведём следующие действия:

  • Из строки № 2 вычтем строку № 1 умноженную на 3 (Строка 2 - 3 × строка 1)
  • Из строки № 3 вычтем строку № 1 (Строка 3 - строка 1)

Получим:

1
2
3
0
-1
-2
0
1
1
3
-9
-2

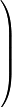Проведём следующие действия:

  • Строку № 2 умножим на -1 (Строка 2 = -1 × строка 2 )
  • Из строки № 3 вычтем строку № 2 (Строка 3 - строка 1)

Получим:

1
2
3
0
1
2
0
0
-1
3
9
-11

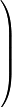Проведём следующие действия:

  • Строку № 3 умножим на -1 (Строка 3 = -1 × строка 3 )
  • Из строки № 2 вычтем строку № 3 умноженную на 2 (Строка 2 - 2 × строка 3)
  • Из строки № 1 вычтем строку № 3 умноженную на 3 (Строка 1 - 3 × строка 3)

Получим:

1
2
0
0
1
0
0
0
1
-30
-13
11

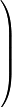Проведём следующие действия:

  • Из строки № 1 вычтем строку № 2 умноженную на 2 (Строка 1 - 2 × строка 2)

Получим:

1
0
0
0
1
0
0
0
1
-4
-13
11

В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:
х1 = -4
х2 = -13
х3 = 11


Вы поняли, как решать? Нет?

Другие примеры

Привет.
Я Настя из ИвГУ (это город Иваново).

«Сегодня от своего лица хочу поблагодарить этот сайт за помощь мне с учебой. Здесь я пользовалась не только материалами, но и нашла преподавателей которые решали мне задачи.

Если тебе нужно что-то сделать в универе, я сама рекомендую. А также пользуйся моей ссылкой и получай 300 руб. на счёт при регистрации.»

Пунктуация и орфография автора сохранены

Получить 300 руб. от Насти

Webmath — преподаватель со стажем более 5 лет выполнит учебную работу за вас

Договор

Строго соблюдаем условия договора от заказа до защиты

Наши авторы

10 000+ преподавателей и научных сотрудников

Гарантии

Точное соответствие ТЗ с бесплатными доработками

АкцияСкидка 25% на вашу работу + речь в подарок. Дарим вам 100₽ на первый заказ!