Мощностью некоторой силы является скалярная физическая величина, которая характеризует скорость произведения работы данной силой. Мощность часто обозначают буквами: N, P.
$$P=\frac{\Delta A}{\Delta t}(1)$$Содержание:
Определение и формулы мощности
Определение
В том случае, если за равные малые промежутки времени выполняется разная работа, то мощность является переменной во времени. Тогда вводят мгновенное значение мощности:
$$P=\lim _{\Delta t \rightarrow 0} \frac{\delta A}{\Delta t}=\frac{d A}{d t}$$где $\delta A$ – элементарная работа, которую выполняет сила, $\Delta t$ – отрезок времени в течение, которого данная работа была выполнена. Если мгновенная мощность не является постоянной величиной, то выражение (1) определяет среднюю мощностьза время $\Delta t$.
Мощность силы можно определить как скалярное произведение силы на скорость, с которой движется точка приложения рассматриваемой силы:
$$P=\bar{F} \bar{v}=F_{\tau} v$$где $F_{\tau}$ – проекция силы $\bar{F}$ на направление вектора скорости ( $\bar{v}$).
При поступательном движении некоторого тела, имеющего массу m под воздействием силы $\bar{F}$ мощность можно вычислить, применяя формулу:
$$P=m v \dot{v}(4)$$В общем случае произвольного перемещения твердого тела суммарная мощность есть алгебраическая сумма мощностей всех сил, которые действуют на тело:
$$P=\sum_{i=1}^{k} \bar{F}_{i} \cdot \bar{v}_{i}(5)$$где $\bar{v}_{i}$ – скорость перемещения точки, к которой приложена сила $\bar{F}_{i}$.
В случае поступательного движения твердого тела со скоростью $\bar{v}$ мощность можно определить при помощи формулы:
$$P=\overline{F v}(6)$$где $\bar{F}$ – главный вектор внешних сил.
Если твердое тело совершает вращение вокруг точки О или вокруг неподвижной оси, которая проходит через точку О, то формулой для счет мощности можно считать выражение:
$$P=\bar{M} \bar{\omega}(7)$$где $\bar{M}$ – главный момент внешних сил по отношению к точке О, $\bar{omega}$ – мгновенная угловая скорость вращения тела.
Единицы измерения мощности
Основной единицей измерения мощности силы в системе СИ является: [P]=вт (ватт)
В СГС: [P]=эрг/с.
1 вт=107 эрг/( с).
Примеры решения задач
Пример
Задание. Какова мощность (P(t)), развиваемая силой, если она действует на тело, которое имеет массу m и под воздействием приложенной силы движется поступательно. Сила описывается законом: $F(t)=2 t \cdot \bar{i}+3 t^{2} \bar{j}$
Решение. В качестве основы для решения задачи используем формулу для мощности вида:
$$P=F \cdot v(1.1)$$Из второго закона Ньютона мы имеем:
$$F=m a \rightarrow a=\frac{F}{m} ; v=\int a d t=\int \frac{F}{m} d t=\frac{1}{m} \int F d t(1.2)$$В выражение (2.2) подставим уравнение, заданное в условии задачи для F(t), имеем:
$$v=\frac{1}{m} \int\left(2 t \cdot \bar{i}+3 t^{2} \bar{j}\right) d t=\frac{1}{m}\left(t^{2} \cdot \bar{i}+t^{3} \bar{j}\right)(1.3)$$Подставим выражение для скорости из (1.3) в (1.1), получим:
$$P=\left(2 t \cdot \bar{i}+3 t^{2} \bar{j}\right) \frac{1}{m}\left(t^{2} \cdot \bar{i}+t^{3} \bar{j}\right)=\frac{1}{m}\left(2 t^{3}+3 t^{5}\right)$$Ответ. $P=\frac{1}{m}\left(2 t^{3}+3 t^{5}\right)$
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Пример
Задание. Какова мгновенная мощность силы тяжести на высоте h/2. если камень массы m падает с высоты h. Сопротивление воздуха не учитывать.
Решение. Сделаем рисунок.
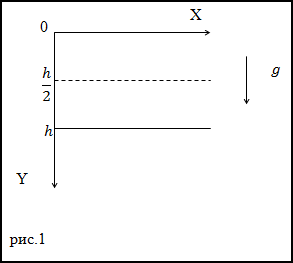
В качестве основы для решения задачи используем формулу для мгновенной мощности вида:
$$P=\bar{F} \cdot \bar{v}(2.1)$$Сила, действующая на тело – сила тяжести. Она направлена по оси Y, выражение для ее проекции на ось Y запишем как:
$$F=m g(2.2)$$В начальный момент времени тело имело скорость равную нулю, тогда скорость тела в проекции на ось Y можно вычислить, используя выражение:
$$v=v_{0}+g t=g t(2.3)$$где v0=0.
Найдем момент времени, в который тело окажется на половине высоты (y=h/2), применим уравнение, которое описывает равноускоренное движение (из начальных условий y0=0, v0=0):
$$y=y_{0}+v_{0} t+\frac{g t^{2}}{2}=\frac{g t^{2}}{2}=\frac{h}{2} \rightarrow t=\sqrt{\frac{h}{g}}(2.4)$$Используем выражения (2.2), (2.3), (2.4) подставим в (2.1), получим искомую мгновенную мощность силы тяжести на половине пути свободно падающего тела:
$$P=m g \cdot g \sqrt{\frac{h}{g}}=m \sqrt{g^{3} h}$$Ответ. $P=m \sqrt{g^{3} h}$
Читать дальше: Формула плотности вещества.
Статьи по теме
Поможем выполнить
любую работу
