Содержание:

Электрический ток, на каком угодно участке цепи совершает некоторую работу (А). Допустим, что у нас есть произвольный участок цепи (рис.1) между концами которого имеется напряжение U.

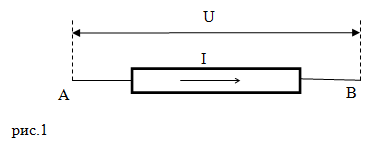
Работа, которая выполняется при перемещении заряда равного 1 Кл между точками A и B (рис.1) будет равна U. В том случае, если через проводник протекает ток силой I за время равное $\Delta t$ по указанному выше участку пройдет заряд (q) равный:

$$q=I \Delta t(1)$$

Следовательно, работа, которую совершает электрический ток на данном участке, равна:

$$A=U \cdot I \cdot \Delta t(2)$$

Надо отметить, что выражение (2) является справедливым при I=const для любого участка цепи (в таком участке могут содержаться проводники 1–го и 2–го рода).

Определение и формула мощности тока

Определение

Мощность тока – есть работа тока в единицу времени:

$$P=\frac{A}{\Delta t}$$

Формулой для вычисления мощности можно считать выражение:

$$P=U \cdot I=I^{2} R(4)$$

В том случае, если участок цепи содержит источник тока, то формулу мощности можно представить в виде:

$$P=\left(\varphi_{1}-\varphi_{2}\right) I+\varepsilon I$$

где $\left(\varphi_{1}-\varphi_{2}\right)$ – разность потенциалов, $\varepsilon$ – ЭДС источника, который включен в цепь.

Выражение (5) является интегральной записью. Это выражение можно представить в дифференциальной форме, если использовать понятие удельной мощности ($P_{u d}=\frac{\Delta P}{\Delta V}$ – мощность, развиваемая током в единице объема проводника):

$$P_{u d}=\rho j^{2}(6)$$

где j – плотность тока, $\rho$ – удельное сопротивление.

Единицы измерения мощности тока

Основной единицей измерения мощности тока (как и мощности вообще) в системе СИ является: [P]=Вт=Дж/с.

В СГС: [P]=эрг/с.

1 Вт=107 эрг/( с).

Выражение (4) применяют в системе СИ для того, чтобы дать определение единицы напряжения. Так, единицей напряжения (U) является вольт (В), который равен: 1 В= (1 Вт)/(1 А).

Вольтом называют электрическое напряжение, которое порождает в электроцепи постоянный ток силы 1 А при мощности 1 Вт.

Примеры решения задач

Пример

Задание. Какой должна быть сила тока, которая течет через обмотку электрического мотора для того, чтобы полезная мощность двигателя (PA) стала максимальной?Какова максимальная полезная мощность? Если двигатель постоянного тока подключен к напряжению U, сопротивление обмотки якоря – R.

Решение. Мощность, которую потребляет электроприбор, идет на нагревание (PQ) и совершение работы (PA):

$$P=P_{Q}+P_{A}(1.1)$$

Мощность, идущую на нагревание можно рассчитать как:

$$P_{Q}=I^{2} R(1.2)$$

Потребляемую мощность найдем как:

$$P=I U(1.3)$$

Выразим $P_A$ из (1.1) и используем (1.2) и (1.3):

$$P_{A}=I U-I^{2} R$$

Для нахождения экстремума функции, которая представлена в выражении (1.4) найдем производную $\frac{d P_{A}}{d I}$ и приравняем ее к нулю:

$$\frac{d P_{A}}{d I}=\frac{d}{d I}\left(I U-I^{2} R\right) ; U-2 I_{\max } R=0 \rightarrow I_{\max }=\frac{U}{2 R}(1.5)$$

Найдем максимальную полезную мощность,используя выражение (1.4) и Imax:

$$P_{A \max }=\frac{U}{2 R} U-\left(\frac{U}{2 R}\right)^{2} R=\frac{U^{2}}{4 R}$$

Ответ. $I_{\max }=\frac{U}{2 R} . P_{\text {Amax}}=\frac{U^{2}}{4 R}$


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 467 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Электрические лампочкис мощностями P1 и P2 номинальным напряжением U1=U2 соединяют последовательно (рис.2) и включают в сеть с постоянным напряжением U. Какова мощность, потребляемая первой лампочкой P1*).

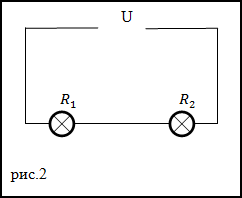
Решение. Лампочки по условию задачи соединены последовательно, значит сила тока, текущая через лампочки одинакова, а падение напряжения на каждой из лампочек зависит от их сопротивлений. Искомую мощность можно найти как:

$$P_{1}^{*}=I^{2} R_{1}(2.1)$$

Сопротивления лампочек можно найти из данных в условиях номинальных мощностей:

$$R_{1}=\frac{U_{1}^{2}}{P_{1}} ; R_{2}=\frac{U_{2}^{2}}{P_{2}}(2.2)$$

Силу тока можно найти по закону Ома, учитывая, что лампочки соединены последовательно:

$$I=\frac{U}{R_{1}+R_{2}}(2.3)$$

Решая уравнения (2.1) – (2.3) совместно получим:

$$P_{1}^{*}=\frac{U^{2} U_{1}^{2}}{U_{1}^{2}+\frac{P_{1} U_{2}^{2}}{P_{2}}}$$

Читать дальше: Формула напряжения электрического поля.