Установившееся течение идеальной баротропной жидкости в потенциальном поле сил подчиняется уравнению Бернулли:
$$\varphi_{F}+\frac{v^{2}}{2}+\int \frac{d p}{\rho}=C(1)$$Содержание:
- Определение и формула уравнения Бернулли
- Частные случаи уравнения Бернулли
- Следствие уравнения Бернулли
- Примеры решения задач
Определение и формула уравнения Бернулли
При рассмотрении движения жидкости очень часто считают, что перемещение одних частей жидкости относительно других не порождает сил трения. При этом жидкость, у которой вязкость (внутреннее трение) равна нулю, носит название идеальной.
Сжимаемой называют жидкость, плотность которой изменяется и может зависеть от температуры и давления.
Баротропной называют жидкость (или газ), плотность которой валяется функцией давления (не является функцией температуры).
Течение жидкости или газа называют стационарным, если скорость и давление жидкости остаются постоянными в каждой точке жидкости (газа).
Определение
где $\varphi_{F}$ – потенциал поля массовых сил; C – величина постоянная для всех точек, которые принадлежат одной линии тока и переменная при переходе к другой линии тока; $\rho$ – плотность идеальной жидкости; p – давление, v – скорость жидкости.
Частные случаи уравнения Бернулли
При воздействии на жидкость только силы тяжести (нет других массовых сил), то потенциал поля можно представить:
$$\varphi_{F}=g \approx$$где g – ускорение свободного падения, ось OZ имеет направление вверх (z – координата (или высота) по данной оси), тогда уравнение Бернулли можно записать как:
$$g z+\frac{v^{2}}{2}+\int \frac{d p}{\rho}=C(2)$$В том случае, если идеальную жидкость можно считать несжимаемой, уравнение Бернулли применяют в виде:
$$ \begin{array}{l} \rho g z+\frac{\rho v^{2}}{2}+p=C_{1}(3) \\ z+\frac{v^{2}}{2 g}+\frac{p}{\rho g}=C_{2}(4) \end{array} $$где $\frac{\rho v^{2}}{2}$ – называют скоростным напором или динамическим давлением; p – статическое давление в той точке пространства, где расположен центр массы исследуемого элемента жидкости; $\frac{p^{\prime}}{\rho g}$ – носит название пьезометрической высоты; $\frac{v^{2}}{2 g}$ – скоростная высота, z – высота на которой находится элемент жидкости, который рассматривается.
Расчеты, которые проводят для реальных жидкостей с применением уравнения Бернулли, дают неплохие результаты.
Следствие уравнения Бернулли
1. Пусть все точки текущей жидкости имеют одинаковые величины скоростей. В таком случае для любых произвольных точек, относящихся к одной линии тока, выполняется равенство:
$$p_{1}-p_{2}=\rho g\left(z_{2}-z_{1}\right)(5)$$где p1 и p2 – давления в точках жидкости, находящихся на высоте z1 и z2, соответственно по вертикальной оси OZ.
Выражение (5) означает, что распределение давления является таким же, как в жидкости, находящейся в покое.
2. Для линии тока, если она горизонтальна уравнение Бернулли (3) примет вид:
$$\frac{\rho v^{2}}{2}+p=C_{1}(6)$$что означает: давление оказывается меньше там, где скорость больше.
Примеры решения задач
Пример
Задание. Какова скорость течения воды в горизонтальной трубе рис.1? Если в манометрических трубках, указанных на том же рис.1 разность уровней жидкости равна h. Считайте, что диаметры трубок одинаковы.
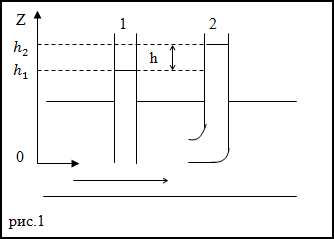
Решение. В качестве основы для решения задачи используем уравнение Бернулли в виде:
$$\rho g z+\frac{\rho v^{2}}{2}+p=C_{1}(1.1)$$Запишем уравнение Бернулли для трубки тока в месте нахождения манометрических трубок (1) и (2) (используем (1.1)):
$$\frac{\rho v^{2}}{2}+p_{2}=p_{1}(1.2)$$Для линии тока при постоянной скорости течения жидкости выполняется:
$$p_{1}-p_{2}=\rho g\left(h_{2}-h_{1}\right)(1.3)$$Значит, получим:
$$\frac{\rho v^{2}}{2}=\rho g\left(h_{2}-h_{1}\right)=\rho g h \rightarrow v=\sqrt{2 g h}$$Ответ. $v=\sqrt{2 g h}$
Пример
Задание. Используя уравнение Бернулли для идеальной несжимаемой жидкости, рассматривая истечение ее из маленького отверстия в широком открытом сосуде, получите формулу Торричелли: $v=\sqrt{2 g h}$, где h=h2-h1 - высота открытой поверхности жидкости над отверстием, v – скорость истечения жидкости из отверстия.
Решение. Сделаем рисунок.
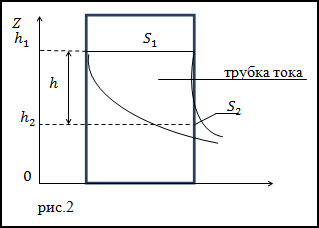
Рассмотрим рис.2. Выделим в жидкости трубку тока с сечениями S1 – площадь открытой поверхности жидкости, S2 – площадь сечения струи из отверстия. Будем считать, что для всех точек каждого из данных сечений скорость жидкости (v) и высота (h) над избранным начальным уровнем одинаковы. Значит к рассматриваемым сечениям применимо уравнение Бернулли:
$$\rho g z+\frac{\rho v^{2}}{2}+p=C_{1}(2.1)$$где для двух рассматриваемых сечений давления p1=p2=p (p - атмосферное давление), скоростью перемещения открытой поверхности можно пренебречь, так как она мала. Уравнение (2.1) двух сечений трубки тока в таком случае упрощается до равенства:
$$\rho g h_{1}=\frac{\rho v^{2}}{2}+\rho g h_{2} \rightarrow \frac{v^{2}}{2}=g h_{2}-g h_{1} \rightarrow v=\sqrt{2 g h}(2.2)$$здесь v – скорость, с которой вытекает жидкость из отверстия.
Что требовалось получить.
Читать дальше: Формула ЭДС.










