Удельным весом называют физическую величину равную весу (P) единицы объема (V) однородного тела. Удельный вес обозначают по-разному, чаще всего встречается буква $\gamma$. Математическая запись определения рассматриваемой нами физической величины выглядит следующим образом:
$$\gamma=\frac{P}{V}(1)$$Содержание:
Определение и формула удельного веса
Определение
Подчеркнем, чтовес тела (P) - это сила, которая появляется в результате воздействия тела на опору или подвес, которая возникает в поле сил тяжести.
Так как вес тела, находящегося в состоянии покоя или равномерного прямолинейного движения совпадает с силой тяжести $(\bar{P}=m \bar{g})$, удельный вес может быть выражен через плотность вещества как:
$$\gamma=\rho g(2)$$где g – модуль ускорение свободного падения.
Удельный вес нельзя назвать физико-химической характеристикой вещества, так как он в соответствии с формулой (2) зависит от ускорения свободного падения и, следовательно,связан, например, с географической широтой места измеренияg. Известно, что на поверхности Земли ускорение свободного падения изменяется в пределах: $9,78 \leq g \leq 9,832$ (м/с2)
Особое внимание следует обратить на то, что удельный вес – это не тоже самое, что плотность вещества ($\rho$), точно так же как масса тела не тоже самое, что вес тела. Это очевидно уже из формулы (2).
Единицы измерения удельного веса
Основной единицей измерения удельного веса в системе СИ является: [$\gamma$]=Н/м3
В СГС: [$\gamma$]=дин/(см3)
1 Н/м3 =0,1дин/(см3)
Примеры решения задач
Пример
Задание. Вычислитеудельный вес смеси, если одна компонента смеси жидкостей имела объем V1=50 л и плотность $\rho_1$=800 кг/м3 , вторая составная часть была объемом V2=55 л и плотностью $\rho_2$=1000 кг/м3 . Считайте, что результирующий объем смеси равен сумме объемов смешиваемых компонент. Ускорение свободного падения принять равным g=9,8 м/с2 .
Решение. Найдем массы компонент смеси (m1,m2), для этого применим формулу:
$$m=\rho V(1.1)$$Соответственно (1.1) получим:
$$m_{1}=\rho_{1} V_{1}, m_{2}=\rho_{2} V_{2}(1.2)$$Переведем объемы веществ из условий задачи в единицы системы СИ, получим: V1=50 л=0,05 м3, V2=55 л=0,055 м3. Рассчитаем массы:
$$ \begin{array}{c} m_{1}=800 \cdot 0,05=40(\mathrm{~K} \Gamma) \\ m_{2}=1000 \cdot 0,055=55(\mathrm{Kr}) \end{array} $$Найдем суммарный объем смеси (V):
$$ V=V_{1}+V_{2}=0,05+0,055=0,105\left(\mathrm{~m}^{3}\right) $$Определим, какова масса смеси:
$$m=m_{1}+m_{2}=40+55=95$ (кг)$Найдём плотность смеси:
$$\rho=\frac{m}{V}=\frac{95}{0,105} \approx 905\left(\mathrm{Kr} / \mathrm{M}^{3}\right)$$Удельный вес смеси найдем, применяя формулу:
$$\gamma=\rho g(1.3)$$Вычислим $\gamma$:
$\gamma=905 \cdot 9,8=8869$ (Н/м3)
Ответ. $\gamma=905 \cdot 9,8=8869$ (Н/м3)
Пример
Задание. Каков удельный вес однородного куска стали ( $\rho$=7,8•108 кг/м3), который находится в кабине космического корабля, совершающего мягкую посадку на Луну? Корабль движется равнозамедленно и вертикально по отношению к поверхности планеты (a=8,38 м/с2), Ускорение свободного падения около поверхности Луны принять равным gL=1,62 м/с2 .
Решение. Сделаем рисунок.
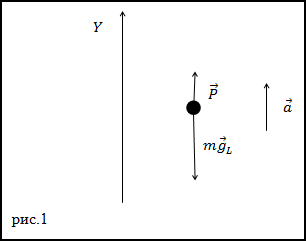
Запишем второй закон Ньютона, для сил, действующих на тело, рассматриваемое в задаче:
$$m \bar{g}_{L}+\bar{P}=m \bar{a}(2.1)$$Запишем проекцию уравнения (2.1) на ось Y:
$$-m g_{L}+P=m a(2.2)$$Выразим модуль веса тела из формулы (2.2), получим:
$$P=m a+m g_{L}=m\left(a+g_{L}\right)(2.3)$$Удельный все тела вычислим применяя его определение:
$$\gamma=\frac{P}{V}(2.4)$$Подставим в выражение (2.4) найденный вес тела (2.3):
$$\gamma=\frac{m\left(a+g_{L}\right)}{V}=\rho\left(a+g_{L}\right)$$Все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
$\gamma=7,8 \cdot 10^{8} \cdot(8,38+1,62)=7,8 \cdot 10^{9}$ (Н/м3)
Ответ. $\gamma=7,8 \cdot 10^{9}$ (Н/м3)
Читать дальше: Формула уравнения Бернулли.










