Длиной пути называют сумму длин всех участков траектории, которые прошла точка за рассматриваемый промежуток времени от t1 до t2.
Содержание:
- Определение и формула пути
- Виды движения и формулы длины пути
- Единицы измерения пути
- Примеры решения задач
Определение и формула пути
Линия, которую описывает материальная точка при своем движении, называется траекторией.
Определение
В том случае, если уравнения движения представлены в прямоугольной декартовой системе координат, то длина пути (s) определяется как:
$$s=\int_{t_{1}}^{t_{2}} \sqrt{\left(\frac{d x}{d t}\right)^{2}+\left(\frac{d y}{d t}\right)^{2}+\left(\frac{d z}{d t}\right)^{2}} d t=\int_{t_{1}}^{t_{2}} \sqrt{(\dot{x})^{2}+(\dot{y})^{2}+(\dot{z})^{2}} d t(1)$$В цилиндрических координатах длина пути может быть выражена как:
$$s=\int_{t_{1}}^{t_{2}} \sqrt{\left(\frac{d \rho}{d t}\right)^{2}+\left(\rho \frac{d \varphi}{d t}\right)^{2}+\left(\frac{d z}{d t}\right)^{2}} d t=\int_{t_{1}}^{t_{2}} \sqrt{(\dot{\rho})^{2}+(\rho \dot{\varphi})^{2}+(\dot{z})^{2}} d t(2)$$В сферических координатах формулу длины пути запишем:
$$s=\int_{t_{1}}^{t_{2}} \sqrt{\left(\frac{d r}{d t}\right)^{2}+\left(r \frac{d \theta}{d t}\right)^{2}+\left(r \sin \theta \frac{d \varphi}{d t}\right)^{2}} d t=\int_{t_{1}}^{t_{2}} \sqrt{(\dot{r})^{2}+(r \dot{\theta})^{2}+(r \varphi \sin \theta)^{2}} d t(3)$$Местоположение перемещающейся материальной точки в фиксированный момент времени, например t=t1 называют начальным положением. Очень часто полагают t1=0. Длин пути, который прошла материальная точка из начального положения – скалярная функция времени: s=s(t).
Считают, что за промежуток времени $d t \rightarrow 0$ материальная точка проходит путь ds, который называют элементарным. При этом:
$$d s=|d \bar{r}|=v d t$$где $\bar{r}$ – вектор элементарного перемещения материальной точки, v – модуль скорости ее движения.
Виды движения и формулы длины пути
Длина пути при равномерном движении (v=const) точки равна:
$$s=v\left(t_{2}-t_{1}\right)(5)$$где t1 – начало отсчета движения, t2 – окончание отсчета. Формула (5) показывает то, что длина пути, который проходит равномерно движущаяся материальная точка – это линейная функция времени.
Если движение не является равномерным, то можно длину пути $\Delta s$ на отрезке времени от $t$ до $t + \Delta t$ находят как:
$$\Delta s=\langle v\rangle \Delta t(6)$$где $\langle v\rangle$ – средняя путевая скорость. При равномерном движении $\langle v\rangle = v$ .
Путь, который проходит материальная тоска при равнопеременном движении (a=const)вычисляют как:
$$s=v_{0} t+\frac{a t^{2}}{2}(7)$$где a – постоянное ускорение, v0 – начальная скорость движения.
Единицы измерения пути
Основной единицей измерения пути в системе СИ является: [s]=м
В СГС: [s]=см
Примеры решения задач
Пример
Задание. Траектория движения материальной точки изображена на рис. 1. Каков путь, пройденный точкой, чему равно перемещение, если точка двигалась 1-2-3-4.
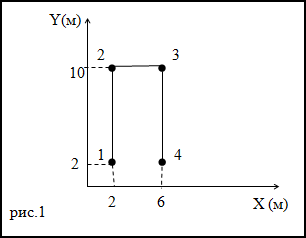
Решение. Перемещение – кратчайшее расстояние между точками 1 и 4. Следовательно, перемещение точки равно:
$$6 - 2 = 4 (m)$$Путь – длина траектории. Рассматривая график на рис.1 получаем, что путь материальной точки равен:
$$8 + 4 + 8 = 20 (m)$$Ответ. Путь равен 20 м, перемещение равно 4 м.
Пример
Задание. Уравнение движения материальной точки в прямоугольной декартовой системе координат представлено функцией: x=-0,2t2 (м) . Какой путь пройдет материальная точка за 5 с?
Решение. Так как уравнение движения задано только одной координатой, то в качестве основы для решения задачи примем формулу пути в виде:
$$s=\int_{t_{1}}^{t_{2}} \sqrt{(\dot{x})^{2}} d t(2.1)$$Подставим в (2.1) функцию x=-0,2t2, учтем, что $0 c \leq t \leq 5 c$ имеем:
$$s=\int_{0}^{5} \sqrt{\left(-0,2 \frac{d\left(t^{2}\right)}{d t}\right)^{2}} d t=0,\left.4 \cdot \frac{t^{2}}{2}\right|_{0} ^{5}=5(m)$$Ответ. s=5м.
Читать дальше: Формула равноускоренного движения.










