Силой называют векторную величину, которая характеризует взаимодействия тел. Ее модуль определяет «степень» (интенсивность) воздействия. Направление силы совпадает с направлением ускорения, которое приобретает тело при взаимодействии с другими телами.
Содержание:
Определение и формула силы
Определение
Силы способны изменять скорости тел и вызывать их деформации. Примером деформированного тела служит сжатая (растянутая) пружина.
Две силы считают равными по модулю и противоположными по направлению, если они приложены к одному телу, но ускорение такого тела равно нулю.
Второй закон Ньютона
Равнодействующая всех сил приложенных к телу (векторная сумма всех сил) ($\bar{F}$) равна производной от импульса тела по времени:
$$\bar{F}=\sum_{i=1}^{n} \bar{F}_{i}=\frac{d \bar{p}}{d t}(1)$$где $\bar{p}=m \bar{v}$ - импульс тела, m–масса рассматриваемого тела, $\bar{v}$ - скорость. Надо отметить, что уравнение (1) строго применимо только относительно материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.
Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней (второй закон Ньютона) можно представить в виде:
$$\bar{F}=m \frac{d \bar{v}}{d t}=m \bar{a}(2)$$где $\bar{a}$ – ускорение, которое материальная точка приобретает в результате воздействия на нее силы. Выражение (2) показывает то, что если $\bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.
Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:
$$F=\frac{\Delta p}{\Delta t}=\frac{m\left(v_{2}-v_{1}\right)}{t_{2}-t_{1}}$$Единицы измерения силы
Основной единицей измерения момента силы в системе СИ является: [F]=Н=(кг•м)/с2
В СГС: [F]=дин
1Н=105 дин
Примеры решения задач
Пример
Задание. Уравнения $x=\alpha t^{3}, y=\beta t$ ($\alpha$ и $\beta$ – постоянные коэффициенты) задают движение материальной точки массы m=const. Как изменяется по модулю сила, которая действует на точку?
Решение. В качестве основы для решения задачи используем второй закон Ньютона в виде:
$\bar{F} = m\bar{a} (1.1)$Зная законы изменения координат точки в зависимости от времени определим уравнения изменения составляющих ускорения. Для этого найдем производные по времени от соответствующих координат:
$$ \begin{array}{c} a_{x}=\frac{d^{2} x}{d t^{2}}=6 \alpha t(1.2) \\ a_{y}=\frac{d^{2} y}{d t^{2}}=0(1.3) \end{array} $$Так как модуль ускорения равен:
$$a=\sqrt{a_{x}^{2}+a_{y}^{2}}(1.4)$$то, учитывая выражения (1.2) и (1.3), получаем:
$a = 6 \alpha t (1.5)$Так как ay=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение и силы совпадают, а мы получили:
$$\bar{a}=6 \alpha t \cdot \bar{i}(1.6)$$где $\bar{i}$ – единичный вектор, направленный по оси X.
Исходя из второго закона Ньютона, имеем:
$$F=m \cdot 6 \alpha t, \bar{F}=m 6 \alpha t \cdot \bar{i}$$Ответ. Так как $F=m \cdot 6 \alpha t$, то с течением времени сила увеличивается по модулю.
Пример
Задание. Два параллелепипеда лежат на горизонтальной поверхности. Они соприкасаются. Данные тела могут скользить по поверхности опоры без трения. Масса одного тела равна m1, второго - m2. Первое тело толкнули с силой F0. Какова сила давления тел друг на друга (F)?
Решение. Сделаем рисунок.
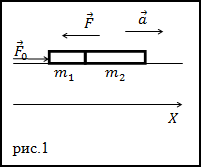
Рассмотрим, какие силы приложены к первому телув момент толчка, запишем для него второй закон Ньютона:
$$\bar{F}_{0}+\bar{F}+m_{1} \bar{g}+\bar{N}=m_{1} \bar{a}(2.1)$$где $m_{1} \bar{g}$ – сила тяжести, $\bar{N}$ – реакция опоры, $\bar{a}$ – ускорение тела.
В проекции на ось Xуравнение (2.1) примет вид:
$$F_{0}-F=m_{1} a \rightarrow F=F_{0}-m_{1} a(2.2)$$Рассмотрим силы, приложенные к двум параллелепипедам как системе:
$$\bar{F}_{0}+\left(m_{1}+m_{2}\right) \bar{g}+\overline{N^{\prime}}=\left(m_{1}+m_{2}\right) \bar{a}(2.3)$$В проекции на ось X уравнение (2.3) примет вид:
$$F_{0}=\left(m_{1}+m_{2}\right) a(2.4)$$Из уравнения (2.4) выразим ускорение:
$$a=\frac{F_{0}}{m_{1}+m_{2}}$$Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:
$$F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$$Ответ. $F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$
Читать дальше: Формула сопротивления.










