Равнодействующую сил давления на тело, которое погружено в жидкость или газ называют выталкивающей силой. Выталкивающая сила может быть больше, чем сила тяжести, которая действует на тело. Силы выталкивания появляются и в том случае,если тело находится в жидкости или газе частично.
Содержание:
На поверхность тела, которое находится в жидкости или газе действуют силы давления. Известно, что давление увеличивается с увеличением глубины погружения. Значит, что силы давления, которые действуют на нижнюю часть тела и направлены вверх больше по модулю, чем силы, которые действуют на верхнюю часть тела и направлены вниз.
Определение и формула силы выталкивания
Определение
Если тело, находящееся в жидкости оставить в покое, то оно тонет, находится в равновесии или всплывает на поверхность.
Это зависит от соотношения силы тяжести и выталкивающей силы (FA),действующих на тело. В первом случае (тело тонет)
mg>FA . Если mg=FA, то тело находится в равновесии. При mg
На тело, погруженное в жидкость или газ, действует сила выталкивания (сила Архимеда FA), равная весу вытесненной им жидкости или газа. В математическом виде данный закон выглядит как:
$$F_{A}=\rho V g$$где $\rho$ – плотность жидкости (газа), в которую погружено тело, g=9,8 м/с2 – ускорение свободного падения, V – объем тела (его части), которое находится в жидкости (газе). Сила Архимеда приложена к центру тяжести объема части тела, которая находится в жидкости (газе).
Закон Архимеда можно применять для вычисления плотности однородного тела неправильной формы. При этом тело взвешивают два раза: один раз в воздухе, второй раз, погрузив тело в жидкость, плотность которой известна.
Основной единицей измерения силы Архимеда, как и любой силы в системе СИ является: [FA]=Н
В СГС: FA]=дин
1Н= (кг•м)/с2
Примеры решения задач
Пример
Задание. Какова сила выталкивания, которая действует на куб, погруженный в систему жидкостей. Сосуд наполнен водой, поверх воды налит керосин. Граница раздела жидкостей проходит посередине грани куба. Плотность воды считайте равной $\rho$1=103 кг/м3 , плотность керосина равна $\rho$2=0,81•103 кг/м3 . Сторона куба равна a=0,1 м.
Решение. Сделаем рисунок.
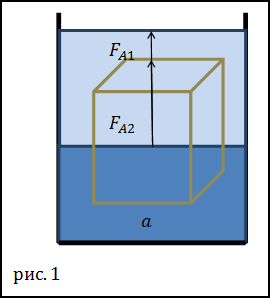
Сила выталкивания, которая действует со стороны воды, на половину куба равна:
$$F_{A 1}=\rho_{1} \frac{V}{2} g$$где V=a3
Сила выталкивания, которая действует со стороны керосина, на половину куба равна:
$$F_{A 2}=\rho_{2} \frac{V}{2} g$$Обе силы направлены вверх. Приложены они к разным точкам (центрам масс объемов тел, погруженных в соответствующие жидкости), при суммировании векторы можно перенести в одну точку параллельно самим себе. Получим, результирующая сила выталкивания равна:
$$F_{A}=F_{A 1}+F_{A 2}(1.3)$$Подставим компоненты силы (1.2), (1.3) в выражение (1.1), имеем:
$$F_{A}=\rho_{1} \frac{a^{3}}{2} g+\rho_{2} \frac{a^{3}}{2} g$$Проведем вычисления:
$$F_{A}=10^{3} \frac{(0,1)^{3}}{2} \cdot 9,8+0,81 \cdot 10^{3} \frac{(0,1)^{3}}{2} \cdot 9,8 \approx 8,8(H)$$Ответ. Ответ: FA=8,8 Н
Пример
Задание. Какова плотность камня, если его вес в воздухе 3,2 Н, а вес в воде 1,8 Н.
Решение. Вес камня в воздухе:
$$P=\rho g V \rightarrow V=\frac{P}{\rho g}$$где $\rho$ – плотность камня, V – объем камня. Взвешивая камень в воде, получаем вес камня в жидкости, равный:
$$P^{\prime}=P-F_{A}(2.2)$$где FA – сила выталкивания (сила Архимеда). В соответствии с законом Архимеда:
$$F_{A}=\rho_{H_{2} O g V}$$где $\rho$H2O – плотность воды. Подставим вместо V выражение (2.1), имеем:
$$F_{A}=\rho_{H_{2} O g} \frac{P}{\rho g}=\frac{\rho_{H_{2} O}}{\rho} P(2.4)$$Подставим в уравнение (2.2) формулу (2.4), получаем:
$$\rho=\frac{P \cdot \rho_{H_{2} O}}{P-P^{\prime}}(2.5)$$Плотность воды будем считать равной $\rho$H2O=103 кг/м3 . Можно провести вычисления:
$\rho=\frac{3,2 \cdot 10^{3}}{3,2-1,8} \approx 2,29 \cdot 10^{3}$ кг/м3
Ответ. Плотность камня $ 2,29 \cdot 10^{3}$ кг/м3
Читать дальше: Формула силы тока.










