Преобразование Лапласа - интегральное преобразование, связывающее функцию F(p) комплексного переменного (изображение) с функцией f(x) действительного переменного (оригинал).
Преобразованием Лапласа от функции f(x) (оргигинала) называется функция:
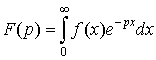
f(x) называют оригиналом преобразования Лапласа, а F(p) - изображением преобразования Лапласа. f(x) и F(p) однозначно определяются друг относительно друга, тоесть если Вы знаете f(x), то всегда можете узнать F(p), и наоборот, если знаете F(p), то всегда можете получить f(x).
Преобразование Лапласа является одним из самых мощных инструментов для решения очень многих задач в области математики, экономики, радиотехники, геометрии, теории управления, микропроцессоров, теории вероятности, теории массового обслуживания и много другого. Часто для решения задачи достаточно получить преобразование Лапласа от искомой функции (именно здесь и пригодится таблица преобразований Лапласа). Также преобразование Лапласа используют при решении задачи Коши для линейного дифференциального уравнения с постоянными коэффициентами, для решения интегральных уравнений, вычисления несобственных интегралов, для представления сигнала в спектральной области и многого другого!
Если в преобразовании Лапласа или таблице преобразований Лапласа Вам что-то не понятно, то Вы всегда можете задать вопрос на нашем форуме, мы будем рады Вам помочь!
Таблица преобразований Лапласа, таблица Лапласа
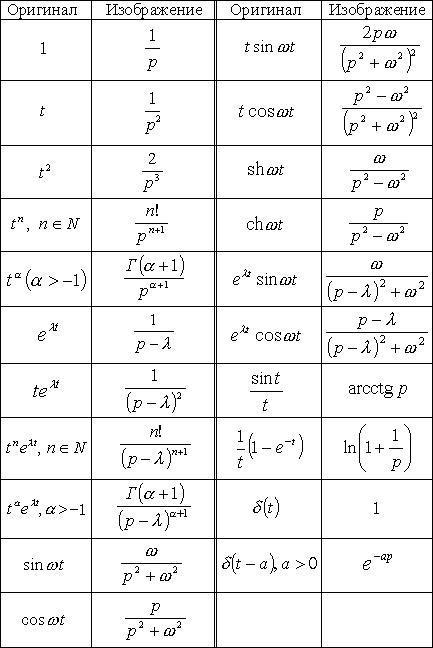
В данный момент продолжается разработка таблицы Лапласа и в ближайшее время будут добавлены новые значения в таблицу преобразований Лапласа.










