Силой трения называют силу, которая возникает при относительном перемещении (или попытке перемещения) тел и является результатом сопротивления движению окружающей среды или других тел.
Содержание:
Определение и формула силы трения
Определение
Силы трения возникают тогда, когда соприкасающиеся тела (или их части) перемещаются относительно друг друга. При этом трение, которое появляется при относительном перемещении соприкасающихся тел, называют внешним. Трение, возникающее между частями одного сплошного тела (газ, жидкость) названо внутренним.
Сила трения – это вектор, который имеет направление вдоль касательной к трущимся поверхностям (слоям). При этом эта сила направлена в сторону противодействия относительному смещению этих поверхностей (слоев). Так, если два слоя жидкости перемещаются друг по другу, при этом движутся с различными скоростями, то сила, которая приложена к слою, перемещающемуся с большей скоростью, имеет направление в сторону, которая противоположна движению. Сила же, которая воздействует на слой, который движется с меньшей скоростью, направлена по движению.
Виды трения
Трение, которое возникает между поверхностями твердых тел, называют сухим. Оно возникает не только при скольжении поверхностей, но и при попытке вызвать перемещение поверхностей. При этом возникает сила трения покоя. Внешнее трение, которое появляется между движущимися телами, называют кинематическим.
Законы сухого трения говорят о том, что максимальная сила трения покоя и сила трения скольжения не зависят от площади поверхностей соприкосновения соприкасающихся тел, подверженных трению. Эти силы пропорциональны модулю силы нормального давления (N), которая прижимает трущиеся поверхности:
$$F_{t r}=\mu N$$где $\mu$ – безразмерный коэффициент трения (покоя или скольжения). Данный коэффициент зависит от природы и состояния поверхностей трущихся тел, например от наличия шероховатостей. Если трение возникает как результат скольжения, то коэффициент трения является функцией скорости. Довольно часто вместо коэффициента трения применяют угол трения, который равен:
$$\operatorname{tg}\varphi=\mu ( 2 )$$Угол $\varphi_{0}=\operatorname{arctg} \mu_{0}$ равен минимальному углу наклона плоскости к горизонту, при котором тело, лежащее на этой плоскости, начинает скользить, под воздействие силы тяжести.
Более точным считают закон трения, который принимает во внимание силы притяжения между молекулами тел, которые подвергаются трению:
$$F_{t r}=\mu_{0}\left(N+S p_{0}\right)(3)$$где S – общая площадь контакта тел, p0 – добавочное давление, которое вызывается силами молекулярного притяжения, $\mu_0$ – истинный коэффициент трения.
Трение между твердым телом и жидкостью (или газом) называют вязким (жидким). Сила вязкого трения становится равной нулю, если скорость относительного движения тел обращается в нуль.
При движении тела в жидкости или газе появляются силы сопротивления среды, которые могут стать существенно больше, чем силы трения. Величина силы трения скольжения зависит от формы, размеров и состояния поверхности тела, скорости движения тела относительно среды, вязкости среды. При не очень больших скоростях сила трения вычисляется при помощи формулы:
$$\bar{F}_{t p}=-\mu^{\prime} \bar{v}(4)$$где знак минус означает, что сила трения имеет направление в сторону противоположную направлению вектора скорости. При увеличении скоростей движения тел в вязкой среде линейный закон (4) переходит в квадратичный:
$$\bar{F}_{t p}=-\mu^{\prime \prime} v^{2} \frac{\bar{v}}{v}(5)$$Коэффициенты $\mu^{\prime}$ и $\mu^{\prime \prime}$ существенно зависимы от формы, размеров, состояния поверхностей тел, вязкости среды.
Помимо этого выделяют трение качения.В первом приближении трение качения рассчитывают, применяя формулу:
$$F_{t r}=k \frac{N}{r}(6)$$где k – коэффициент трения качения, который имеет размерность длины и зависит от материала тел, подверженных контакту и качеств поверхностей и т.д. N – сила нормального давления , r – радиус катящегося тела.
Единицы измерения силы трения
Основной единицей измерения силы трения (как и любой другой силы) в системе СИ является: [P]=H
В СГС: [P]=дин.
Примеры решения задач
Пример
Задание. На горизонтальном диске лежит маленькое тело. Диск вращается вокруг оси, которая проходит через его центр, перпендикулярно плоскости с угловой скоростью $\omega$. На каком расстоянии от центра диска может находиться в состоянии равновесия тело, если коэффициент трения между диском и телом равен $\mu$?
Решение. Изобразим на рис.1 силы, которые будут действовать на тело, положенное на вращающийся диск.
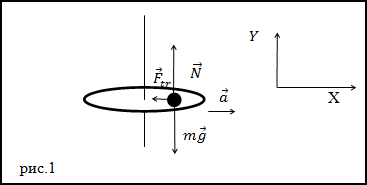
В соответствии со вторым законом Ньютона имеем:
$$m \bar{g}+\bar{F}_{t r}+\bar{N}=m \bar{a}(1.1)$$В проекции на ось Yиз уравнения (1.1) получим:
$$-m g+N=0(1.2)$$В проекции на ось X имеем:
$$-F_{t r}=m a_{n}=m \frac{v^{2}}{r}(1.3)$$где ускорение движения маленького тела равно по модуль нормальной составляющей полного ускорения. Силутрения покоя найдем как:
$$F_{t r}=\mu N$$примем во внимание выражение (1.2), тогда имеем:
$$F_{t r}=\mu \cdot m g(1.5)$$приравняем правые части выражений (1.3) и (1.5):
$$m \frac{v^{2}}{r}=\mu \cdot m g \rightarrow \frac{v^{2}}{r}=\mu g \rightarrow r=\frac{v^{2}}{\mu g}(1.6)$$где маленькое тело (так как оно находится в состоянии покоя на диске) движется со скоростью, равной:
$$v=\omega \cdot r(1.7)$$Следовательно:
$$r=\frac{(\omega \cdot r)^{2}}{\mu g} \rightarrow r=\frac{\mu g}{\omega^{2}}$$Ответ. $r=\frac{\mu g}{\omega^{2}}$
Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
Пример
Задание. По наклонной поверхности равномерно движется тело. Угол наклона плоскости равен $\alpha$. Коков коэффициент трения между телом и наклонной плоскостью?
Решение. Сделаем рисунок.
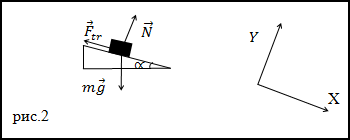
В соответствии со вторым законом Ньютона, учитывая, что движение равномерное, имеем:
$$m \bar{g}+\bar{F}_{t r}+\bar{N}=0(1.1)$$В проекции на ось Y (данная ось параллельна силе реакции опоры) из уравнения (1.1) получим:
$$-m g \cdot \cos (\alpha)+N=0 \rightarrow N=m g \cdot \cos (\alpha)(1.2)$$В проекции на ось X имеем:
$$F_{t r}=m g \cdot \sin (\alpha)(1.3)$$Так как можно принять, что:
$$F_{t r}=\mu N$$то получаем:
$$m g \cdot \sin (\alpha)=\mu m g \cdot \cos (a) \rightarrow \mu=\operatorname{tg}(\alpha)$$Ответ. $\mu=\operatorname{tg}(\alpha)$
Читать дальше: Формула силы тяжести.
Статьи по теме
Поможем выполнить
любую работу
