Формула силы натяжения нити

Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?

Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.

$$\bar{T}+m \bar{g}=m \bar{a}(1.1)$$

где $\bar{T}$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:

$$T-m g=m a(1.2)$$

Из выражения (1.2) получим ускорение:

$$a=\frac{T-m g}{m}$$

Все данные в задаче представлены в единицах системы СИ, проведем вычисления:

$$a=\frac{4400-400 \cdot 9,8}{400}=1,2 \mathrm{~m} / \mathrm{c}^{2}$$

Ответ. a=1,2м/с²

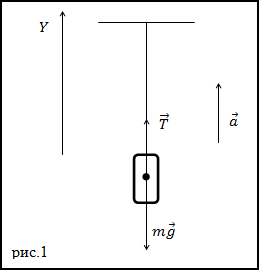
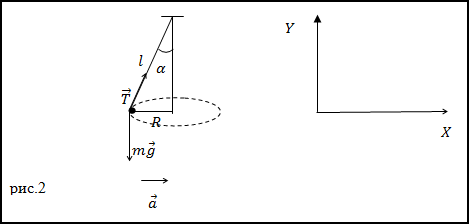Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.

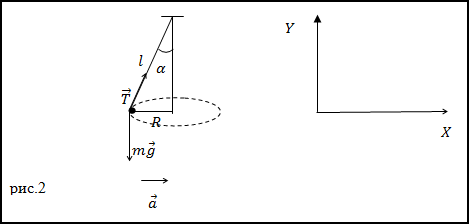
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:

$$\bar{T}+m \bar{g}=m \bar{a}(2.1)$$

Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:

$$ \begin{array}{c} X: \quad T \sin \alpha=m a=m \omega^{2} R(2.2) \\ Y: \quad-m g+T \cos \alpha=0 \end{array} $$

Из уравнения (2.3) получим формулу для модуля силы натяжения нити:

$$T=\frac{m g}{\cos \alpha}(2.4)$$

Из рис.2 видно, что:

$$\sin \alpha=\frac{R}{l} \rightarrow \cos \alpha=\sqrt{1-\left(\frac{R}{l}\right)^{2}}$$

Подставим (2.5) вместо $\cos \alpha$ в выражение (2.4), получим:

$$T=\frac{m g}{\sqrt{1-\left(\frac{R}{l}\right)^{2}}}=\frac{m g l}{\sqrt{l^{2}-R^{2}}}$$

Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:

$$T=\frac{0,1 \cdot 9,8 \cdot 5}{\sqrt{5^{2}-3^{2}}}=1,225(H)$$

Ответ. T=1,225 Н