Содержание:

Определение и формула внутренней энергии

Определение

Внутренней энергией тела (системы) называют энергию, которая связана со всеми видами движения и взаимодействия частиц, составляющих тело (систему), включая энергию взаимодействия и движения сложных частиц.

Из выше сказанного следует, что к внутренней энергии не относят кинетическую энергию движения центра масс системы и потенциальную энергию системы, вызванную действием внешних сил. Это энергия, которая зависит только от термодинамического состояния системы.

Внутреннюю энергию чаще всего обозначают буквой U. При этом бесконечно малое ее изменение станет обозначаться dU. Считается, что dU является положительной величиной, если внутренняя энергия системы растет, соответственно, внутренняя энергия отрицательна, если внутренняя энергия уменьшается.

Внутренняя энергия системы тел равна сумме внутренних энергий каждого отдельного тела плюс энергия взаимодействия между телами внутри системы.

Внутренняя энергия – функция состояния системы. Это означает, что изменение внутренней энергии системы при переходе системы из одного состояния в другое не зависит от способа перехода (вида термодинамического процесса при переходе) системы и равно разности внутренних энергий конечного и начального состояний:

$$\Delta U=U_{2}-U_{1}(1)$$

Для кругового процесса полное изменение внутренней энергии системы равно нулю:

$$\oint d U=0(2)$$

Для системы, на которую не действуют внешние силы и находящуюся в состоянии макроскопического покоя, внутренняя энергия – полная энергия системы.

Внутренняя энергия может быть определена только с точностью до некоторого постоянного слагаемого (U0), которое не определимо методами термодинамики. Однако, данный факт не существенен, так как при использовании термодинамического анализа, имеют дело с изменениями внутренней энергии, а не абсолютными ее величинами. Часто U_0 полагают равным нулю. При этом в качестве внутренней энергии рассматривают ее составляющие, которые изменяются в предлагаемых обстоятельствах.

Внутреннюю энергию считают ограниченной и ее граница (нижняя) соответствует T=0K.

Внутренняя энергия идеального газа

Внутренняя энергия идеального газа зависит только от его абсолютной температуры (T) и пропорциональна массе:

$$U=\int_{0}^{T} C_{V} d T+U_{0}=m\left(\int_{0}^{T} c_{V} d T+u_{0}\right)$$

где CV – теплоемкость газа в изохорном процессе; cV - удельная теплоемкость газа в изохорном процессе; $u_{0}=\frac{U_{0}}{m}$ – внутренняя энергия, приходящаяся на единицу массы газа при абсолютном нуле температур. Или:

$$d U=\frac{i}{2} \nu R d T(4)$$

i – число степеней свободы молекулы идеального газа, v – число молей газа, R=8,31 Дж/(моль•К) – универсальная газовая постоянная.

Первое начало термодинамики

Как известно первое начало термодинамики имеет несколько формулировок. Одна из формулировок, которую предложил К. Каратеодори говорит о существовании внутренней энергии как составляющей полной энергии системы.Она является функцией состояния, в простых системах зависящей от объема (V), давления (p), масс веществ (mi), которые составляют данную систему: $U=U\left(p, V, \sum m_{i}\right)$ . В формулировке, которую дал Каратеодори внутренняя энергия не является характеристической функцией своих независимых переменных.

В более привычных формулировках первого начала термодинамики, например, формулировке Гельмгольца внутренняя энергия системы вводится как физическая характеристика системы. При этом поведение системы определено законом сохранения энергии. Гельмгольц не определяет внутреннюю энергию как функцию конкретных параметров состояния системы:

$$\Delta U=Q-A(5)$$

$\Delta U$ – изменение внутренней энергии в равновесном процессе, Q – количество теплоты, которое получила система в рассматриваемом процессе, A – работа, которую система совершила.

Единицы измерения внутренней энергии

Основной единицей измерения внутренней энергии в системе СИ является: [U]=Дж

Примеры решения задач

Пример

Задание. Вычислите, на какую величину изменится внутренняя энергия гелия имеющего массу 0,1 кг, если его температура увеличилась на 20С.

Решение. При решении задачи считаем гелий одноатомным идеальным газом, тогда для расчетов можно применить формулу:

$$d U=\frac{i}{2} \nu R d T(1.1)$$

Так как мы имеем с одноатомным газом, то $i=3 ; \nu=\frac{m}{\mu}$, молярную массу ($\mu$) возьмем из таблицы Менделеева ($\mu_{H e}=4 \cdot 10^{-3}$ кг/моль). Масса газа в представленном процессе не изменяется, следовательно, изменение внутренней энергии равно:

$$\Delta U=\int_{T_{1}}^{T_{2}} d U=\frac{i}{2} \frac{m}{\mu} R \int_{T_{1}}^{T_{2}} d T=\frac{i}{2} \frac{m}{\mu} R\left(T_{2}-T_{1}\right)$$

где $T_{2}-T_{1}=\Delta T=\Delta t$

Все величины необходимые для вычислений имеются:

$\Delta U=\frac{3}{2} \cdot \frac{0,1}{4 \cdot 10^{-3}} \cdot 20 \cdot 8,31=6,2 \cdot 10^{3}$ (Дж)

Ответ. $\Delta U=6,2 \cdot 10^{3}$ (Дж)


Warning: file_put_contents(./students_count.txt): failed to open stream: Permission denied in /var/www/webmath-q2ws/data/www/webmath.ru/poleznoe/guide_content_banner.php on line 20
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 452 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Идеальный газ расширили в соответствии с законом, который изображен графиком на рис.1. от начального объема V0. При расширении объем сал равен $V=\tau V_{0}$ . Каково приращение внутренней энергии газа в заданном процессе? Коэффициент адиабаты равен $\gamma$.

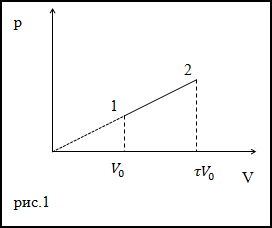
Решение. Исходя из рисунка, уравнение процесса можно представить аналитически как:

$$p=\alpha V(2.1)$$

Показатель адиабаты связан с числом степеней свободы газа выражением:

$$\gamma=\frac{i+2}{i}(2.2)$$

Выразим число степеней свободы из (2.2):

$$i=\frac{2}{\gamma-1}$$

Приращение внутренней энергии для постоянной массы газа (см. Пример 1) найдем в соответствии с формулой:

$$\Delta U=\frac{i}{2} \nu R \Delta T(2.4)$$

Запишем уравнения состояний идеального газа для точек (1) и (2) рис.1:

$$ \begin{aligned} p V &=\nu R T(2.5) \\ p_{0} V_{0} &=\nu R T_{0} \end{aligned} $$

Тогда приращение температуры, учитывая уравнение процесса и выражения (2.5), (2.6) найдем как:

$$ \begin{aligned} \Delta T &=T-T_{0}=\frac{1}{\nu R}\left(p V-p_{0} V_{0}\right)=\frac{1}{\nu R}\left(\alpha V \cdot V-\alpha V_{0} V_{0}\right)=\\ &=\frac{1}{\nu R}\left(\alpha \tau V_{0} \cdot \tau V_{0}-\alpha V_{0} V_{0}\right)=\frac{1}{\nu R} V_{0}^{2} \alpha\left(\tau^{2}-1\right)(2.7) \end{aligned} $$

Подставим $\Delta T$ в выражение для $\Delta U$ (2.4), получим:

$\Delta U=\frac{i}{2} v R \frac{1}{v R} V_{0}^{2} \alpha\left(\tau^{2}-1\right)=\frac{1}{\gamma-1} V_{0}^{2} \alpha\left(\tau^{2}-1\right)$

Ответ. $\Delta U=\frac{1}{\gamma-1} V_{0}^{2} \alpha\left(\tau^{2}-1\right)$


Читать дальше: Формула времени.