Упругой называют деформацию, если после снятия нагрузки прежние размеры тела и его форма полностью восстанавливаются.
Закон Гука
Если на тело воздействовать некоторой силой, то его размер и (или) форма изменяются. Это процесс называют деформацией тела. В телах, подвергающихся деформациям, возникают силы упругости, уравновешивающие внешние силы.
Виды деформации
Все деформации можно разделить на два вида: упругие деформации и пластические.
Пластической считают деформацию, при которой появившиеся, вследствие деформации, изменения размера и формы тела, после снятия нагрузки восстанавливаются частично.
Характер деформации зависит от
- величины и времени воздействия внешней нагрузки;
- материала тела;
- состояния тела (температуры, способов обработки и т.д).
Резкой границы между упругой и пластической деформациями не существует. В большом числе случаев малые и кратковременные деформации можно считать упругими.
Формулировки закона Гука
Эмпирически получено, что чем большую деформацию необходимо получить, тем большую деформирующую силу следует приложить к телу. По величине деформации ($\Delta l$) можно судить о величине силы:
\[\Delta l=\frac{F}{k}\left(1\right),\]выражение (1) означает, что абсолютная величина упругой деформации прямо пропорциональная приложенной силе. Данное утверждение является содержанием закона Гука.
При деформации удлинения (сжатия) тела выполняется равенство:
\[F=k\left(l-l_0\right)=k\Delta l\ \left(2\right),\]где $F$ - деформирующая сила; $l_0$ - начальная длина тела; $l$ - длина тела после деформации; $k$ - коэффициент упругости (коэффициент жесткости, жесткость), $ \left[k\right]=\frac{Н}{м}$. Коэффициент упругости зависит от материала тела, его размеров и формы.
Так как в деформированном теле возникают силы упругости ($F_u$), которые стремятся восстановить прежние размеры и форму телу, то часто закон Гука формулируют относительно сил упругости:
\[F_u=k\left|\Delta l\right|\ \left(3\right).\]Закон Гука хорошо работает для деформаций, которые возникают в стержнях из стали, чугуна, и других твердых веществ, в пружинах. Справедлив закон Гука для деформаций растяжения и сжатия.
Закон Гука для малых деформаций
Сила упругости зависит от изменения расстояния между частями одного и того же тела. Следует помнить, что закон Гука выполняется только для малых деформаций. При больших деформациях сила упругости не пропорциональна измерению длины, при дальнейшем увеличении деформирующего воздействия тело способно разрушаться.
Если деформации тела малы, то силы упругости можно определять по ускорению, которое данные силы сообщают телам. Если тело неподвижно, то модуль силы упругости находят из равенства нулю векторной суммы сил, которые действуют на тело.
Закон Гука можно записывать не только относительно сил, но часто его формулируют для такой величины как напряжение ($\sigma =\frac{F}{S}$ - сила, которая действует на единичную площадь поперечного сечения тела), тогда для малых деформаций:
\[\sigma =Е\frac{\Delta l}{l}\ \left(4\right),\]где $Е$ - модуль Юнга;$\ \frac{\Delta l}{l}$ - относительное удлинение тела.
Примеры задач с решением
Задание. К стальному тросу длинной $l$, диаметром $d$ подвесили груз массой $m$. Каково напряжение в тросе ($\sigma $), а также абсолютное его удлинение ($\Delta l$)?
Решение. Сделаем рисунок.
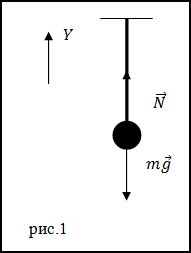
Для того чтобы найти силу упругости, рассмотрим силы, которые действуют на тело, подвешенное к тросу, так как сила упругости будет равна по величине силе натяжения ($\overline{N}$). По второму закону Ньютона имеем:
\[m\overline{g}+\overline{N}=0\ \left(1.1\right).\]В проекции на ось Y уравнения (1.1) получим:
\[N=mg\ \left(1.2\right).\]По третьему закону Ньютона тело, действует на трос с силой равной по величине силе $\overline{N}$, трос, действует на тело с силой $\overline{F}$, равной$\overline{\ N,}$ но противоположного направления, так деформирующая трос сила ($\overline{F}$) равна:
\[\overline{F}=-\overline{N\ }\left(1.3\right).\]Под воздействием деформирующей силы в тросе возникает сила упругости, которая равна по величине:
\[F_u=N=mg\left(1.4\right).\]Напряжение в тросе ($\sigma $) найдем как:
\[\sigma =\frac{F_u}{S}=\frac{mg}{S}\left(1.5\right).\]Площадь S - это площадь поперечного сечения троса:
\[S=\pi \frac{d^2}{4}\left(1.6\right).\]Получим:
\[\sigma =\frac{4mg\ }{{\pi d}^2}\left(1.7\right).\]По закону Гука:
\[\sigma =Е\frac{\Delta l}{l}\left(1.8\right),\]значит:
\[\frac{\Delta l}{l}=\frac{\sigma }{E}\to \Delta l=\frac{\sigma l}{E}\to \Delta l=\frac{4mgl\ }{{\pi d}^2E}.\]Ответ. $\sigma =\frac{4mg\ }{{\pi d}^2};\ \Delta l=\frac{4mgl\ }{{\pi d}^2E}$
Задание. Какова абсолютная деформация первой пружины из двух последовательно соединенных пружин (рис.2), если коэффициенты жесткости пружин равны: $k_1\ и\ k_2$, а удлинение второй пружины составляет $\Delta x_2$?
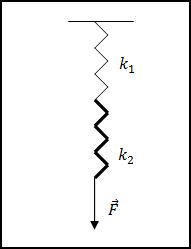
Решение. Если система из последовательно соединенных пружин находится в состоянии равновесия, то силы натяжения данных пружин одинаковы:
\[F_1=F_2=F\ \left(2.1\right).\]По закону Гука:
\[F_1=k_1\Delta x_1;;\ F_2=k_2\Delta x_2\left(2.2\right).\]Согласно (2.1) и (2.2) имеем:
\[k_1\Delta x_1=k_2\Delta x_2\ \left(2.3\right).\]Выразим из (2.3) удлинение первой пружины:
\[\Delta x_1=\frac{k_2\Delta x_2}{k_1}.\]Ответ. $\Delta x_1=\frac{k_2\Delta x_2}{k_1}$.
Читать дальше: закон Паскаля.









